
【题目】如图①,在A、B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶,图②是客车、货车离 C站的路程![]() 、
、![]() (km)与行驶时间x(h)之间的函数图像.
(km)与行驶时间x(h)之间的函数图像.

(1)客车的速度是 km/h;
(2)求货车由 B地行驶至 A地所用的时间;
(3)求点E的坐标,并解释点 E的实际意义.
【答案】(1)60;(2)14h;(3)点E代表的实际意义是在行驶![]() h时,客车和货车相遇,相遇时两车离C站的距离为80km.
h时,客车和货车相遇,相遇时两车离C站的距离为80km.
【解析】
(1)由图象可知客车6小时行驶的路程是360km,从而可以求得客车的速度;
(2)由图象可以得到货车行驶的总的路程,前2h行驶的路程是60km,从而可以起求得货车由B地行驶至A地所用的时间;
(3)根据图象利用待定系数法分别求得EF和DP所在直线的解析式,然后联立方程组即可求得点E的坐标,根据题意可以得到点E代表的实际意义.
解:(1)由图象可得,客车的速度是:360÷6=60(km/h),
故答案为:60;
(2)由图象可得,
货车由B地到A地的所用的时间是:(60+360)÷(60÷2)=14(h),
即货车由B地到A地的所用的时间是14h;
(3)设客车由A到C对应的函数解析式为y=kx+b,
则![]() ,得
,得![]() ,
,
即客车由A到C对应的函数解析式为y=-60x+360;
根据(2)知点P的坐标为(14,360),设货车由C到A对应的函数解析式为y=mx+n,
则![]() ,得
,得![]() ,
,
即货车由C到A对应的函数解析式为y=30x-60;
∴![]() ,得
,得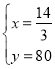 ,
,
∴点E的坐标为(![]() ,80),
,80),
故点E代表的实际意义是在行驶![]() h时,客车和货车相遇,相遇时两车离C站的距离为80km.
h时,客车和货车相遇,相遇时两车离C站的距离为80km.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
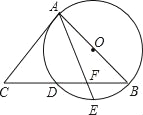
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:①b2=4ac,②abc<0;③a>c;④4a﹣2b+c<0,其中正确的个数有( )
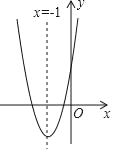
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
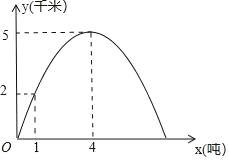
【题目】根据对宁波市相关的市场物价调研,某批发市场内甲种水果的销售利润y1(千元)与进货量x(吨)近似满足函数关系y1=0.25x,乙种水果的销售利润y2(千元)与进货量x(吨)之间的函数y2=ax2+bx+c的图象如图所示.
(1)求出y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种水果共8吨,设乙水果的进货量为t吨,写出这两种水果所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种苗木,由信息解答以下问题:
苗 木 品 种 | A | B | C |
每辆汽车运载量(吨) | 12 | 10 | 8 |
每吨苗木获利(万元) | 3 | 4 | 2 |
(1)设装A种苗木车辆数为x,装运B种苗木的车辆数为y,求y与x之间的函数关系式;
(2)若装运每种苗木的车辆都不少于2辆,则车辆安排方案有几种?写出每种安排方案
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com