
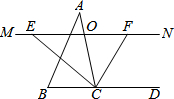
 如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.分析 (1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD及等角对等边即可证得OE=OF;
(2)根据矩形的性质可知:对角线且互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.
解答 (1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)解:当O运动到AC中点时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=$\frac{1}{2}$∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.
点评 此题主要考查了矩形的判定,关键是掌握有一个角为直角的平行四边形是矩形.


科目:初中数学 来源: 题型:选择题
| A. | x2-70x+825=0 | B. | x2+70x-825=0 | C. | x2-140x+3300=0 | D. | x2+140x-3300=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
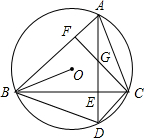 如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且tan∠OBC=1,求四边ABDC的面积.
如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且tan∠OBC=1,求四边ABDC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
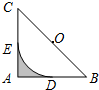 如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠A=90°,AB=AC=2,以BC的中点O为圆心的圆弧分别与AB、AC相切于点D、E,则图中阴影部分的面积是( )| A. | $1-\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{2}$ | D. | $2-\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
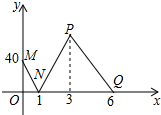 在一条南北方向的航道上依次有A,B,C三个港口,一艘轮船从港口A出发,匀速航行到港口C后返回到港口B,轮船离港口B的距离y(千米)与航行时间x(小时)之间的函数图象如图中的折线MN-NP-PQ所示.已知此次航行过程中水流速度和轮船的静水速度保持不变.
在一条南北方向的航道上依次有A,B,C三个港口,一艘轮船从港口A出发,匀速航行到港口C后返回到港口B,轮船离港口B的距离y(千米)与航行时间x(小时)之间的函数图象如图中的折线MN-NP-PQ所示.已知此次航行过程中水流速度和轮船的静水速度保持不变.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 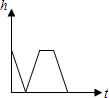 | B. | 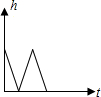 | C. | 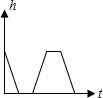 | D. | 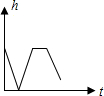 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
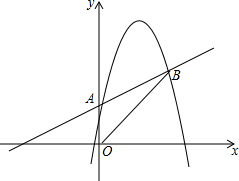 如图,已知抛物线y=-x2+bx+c经过A(0,1)、B(4,3)两点.
如图,已知抛物线y=-x2+bx+c经过A(0,1)、B(4,3)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com