
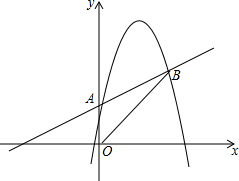
 ��ͼ����֪������y=-x2+bx+c����A��0��1����B��4��3�����㣮
��ͼ����֪������y=-x2+bx+c����A��0��1����B��4��3�����㣮���� ��1����A��B��������������ʽ���ɽ����
��2����ͼ��AM��OB����ΪM������tan��ABO=$\frac{AM}{BM}$�����
��3������MN=BC���г����̼��ɽ����
��4����ͼֻҪ�ж�Gy��Ny���ɣ�
��� �⣺��1��������$\left\{\begin{array}{l}{c=1}\\{-16+4b+c=3}\end{array}\right.$�����$\left\{\begin{array}{l}{b=\frac{9}{2}}\\{c=1}\end{array}\right.$�����������߽���ʽΪy=-x2+$\frac{9}{2}x$+1��
��2����ͼ��AM��OB����ΪM����ֱ��AB�Ľ���ʽΪy=$\frac{1}{2}$x+1��ֱ��OB�Ľ���ʽΪy=$\frac{3}{4}$x��
��ֱ��AMΪy=-2x+1��
��$\left\{\begin{array}{l}{y=\frac{3}{4}x}\\{y=-2x+1}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{4}{11}}\\{y=\frac{3}{11}}\end{array}\right.$��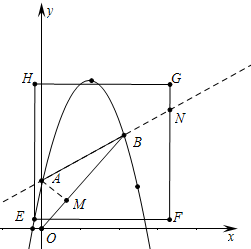
��ֱ�ߵ�M���꣨$\frac{4}{11}$��$\frac{3}{11}$��
��AM=$\frac{4\sqrt{5}}{11}$ BM=$\frac{50}{11}$
��tan��ABO=$\frac{AM}{BM}$=$\frac{2\sqrt{5}}{25}$��
��3�����M����Ϊ��m��-m2+$\frac{9}{2}$m+1������MN��BC��MN=BCʱ��M��N��B��CΪ������ı�����ƽ���ı��Σ�
��|-m2+$\frac{9}{2}$m+1-��$\frac{1}{2}$m+1��|=3��
������m2-4m+3=0��m2-4m-3=0��
���m=1��3��2+$\sqrt{7}$��2-$\sqrt{7}$��
��4����ͼ��FG��ֱ��AB���ڵ�N��
�ߵ�E�ĺ�����Ϊm���ҵ�E�ڵڶ����ޣ�-1��m��0��
�֡�������EFGH�ı߳�Ϊ10��
���F�ĺ�����Ϊa��9��a��10��
��ֱ��AB�Ľ���ʽΪy=$\frac{1}{2}$x+1��
���N��������$\frac{11}{2}$��Ny��6��
�ߵ�G��������11��Gy��10��
��Gy��Ny��
����ڴ��ڻ����-1������ʵ��m��FG�����A��B�����ֱ�߶��н��㣮
���� ���⿼�����ϵ����ȷ�����κ�����һ�κ�������ʽ���������Ǻ����Ķ��壬�����ε����ʵ�֪ʶ��ѧ������ĸm��ʾ��Ӧ�ĵ�������ǽ������Ĺؼ��������ν�ϵ�һ������Ŀ�������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
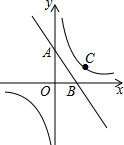 ��ͼ��A��0��4����B��3��0����C��4��2�����ҷ���������ͼ����C��
��ͼ��A��0��4����B��3��0����C��4��2�����ҷ���������ͼ����C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
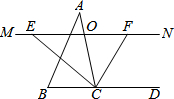 ��ͼ���ڡ�ABC�У���O��AC���ϵ�һ���㣬��O��ֱ��MN��BC����MN����BCA��ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F��
��ͼ���ڡ�ABC�У���O��AC���ϵ�һ���㣬��O��ֱ��MN��BC����MN����BCA��ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
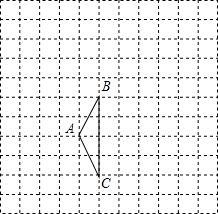 ��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC�Ķ�����ڸ���ϣ��밴Ҫ��������и��⣺
��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC�Ķ�����ڸ���ϣ��밴Ҫ��������и��⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
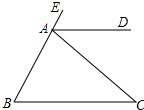 ��ͼ��E��A��B������ͬһֱ���ϣ�ADƽ�֡�EAC��AD��BC����B=50�㣬���C�Ķ���50�㣮
��ͼ��E��A��B������ͬһֱ���ϣ�ADƽ�֡�EAC��AD��BC����B=50�㣬���C�Ķ���50�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
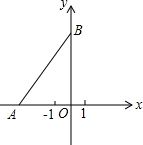 ��ͼ����ƽ��ֱ������ϵ�У���A��-3b��0��Ϊx�Ḻ������һ�㣬��B��0��4b��Ϊy����������һ�㣬����b���㷽�̣�3��b+1��=6��
��ͼ����ƽ��ֱ������ϵ�У���A��-3b��0��Ϊx�Ḻ������һ�㣬��B��0��4b��Ϊy����������һ�㣬����b���㷽�̣�3��b+1��=6���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com