
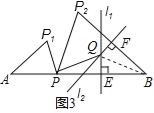
【题目】(12分)已知点P是线段AB上与点A不重合的一点,且AP<PB.AP绕点A逆时针旋转角α(0°<α≤90°)得到AP1,BP绕点B顺时针也旋转角α得到BP2,连接PP1、PP2.

(1)如图1,当α=90°时,求∠P1PP2的度数;
(2)如图2,当点P2在AP1的延长线上时,求证:△P2P1P∽△P2PA;
(3)如图3,过BP的中点E作l1⊥BP,过BP2的中点F作l2⊥BP2,l1与l2交于点Q,连接PQ,求证:P1P⊥PQ.
【答案】(1)90°;(2)见解析;(3)见解析.
【解析】
试题此题主要考查了几何变换综合以及相似三角形的判定和全等三角形的判定与性质等知识,得出Rt△QBE≌Rt△QBF是解题关键.(1)利用旋转的性质以及等腰直角三角形得出∠APP1=∠BPP2=45°,进而得出答案;(2)根据题意得出△PAP1和△PBP2均为顶角为α的等腰三角形,进而得出∠P1PP2=∠PAP2=α,求出△P2P1P∽△P2PA;(3)首先连结QB,得出Rt△QBE≌Rt△QBF,利用∠P1PQ=180°﹣∠APP1﹣∠QPB求出即可.
试题解析:(1)解:由旋转的性质得:AP=AP1,BP=BP2. ∵α=90°,
∴△PAP1和△PBP2均为等腰直角三角形, ∴∠APP1=∠BPP2=45°,
∴∠P1PP2=180°﹣∠APP1﹣∠BPP2=90°;
(2)证明:由旋转的性质可知△PAP1和△PBP2均为顶角为α的等腰三角形, ∴∠APP1=∠BPP2=90°﹣![]() α,
α,
∴∠P1PP2=180°﹣(∠APP1+∠BPP2)=180°﹣2(90°-![]() α)=α,
α)=α,
在△PP2P1和△P2PA中,∠P1PP2=∠PAP2=α, 又∵∠PP2P1=∠AP2P, ∴△P2P1P∽△P2PA.
(3)证明:如图,连接QB. ∵l1,l2分别为PB,P2B的中垂线, ∴EB=![]() BP,FB=
BP,FB=![]() BP2.
BP2.
又BP=BP2, ∴EB=FB. 在Rt△QBE和Rt△QBF中,![]() , ∴Rt△QBE≌Rt△QBF,
, ∴Rt△QBE≌Rt△QBF,
∴∠QBE=∠QBF=![]() ∠PBP2=
∠PBP2=![]() α, 由中垂线性质得:QP=QB, ∴∠QPB=∠QBE=
α, 由中垂线性质得:QP=QB, ∴∠QPB=∠QBE=![]() α,
α,
由(2)知∠APP1=90°﹣![]() α, ∴∠P1PQ=180°﹣∠APP1﹣∠QPB=180°﹣(90°﹣
α, ∴∠P1PQ=180°﹣∠APP1﹣∠QPB=180°﹣(90°﹣![]() α)-
α)-![]() α=90°,
α=90°,
即 P1P⊥PQ.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
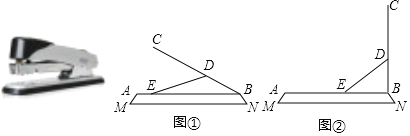
【题目】在日常生活中我们经常会使用到订书机,如图MN是装订机的底座,AB是装订机的托板AB始终与底座平行,连接杆DE的D点固定,点E从A向B处滑动,压柄BC绕着转轴B旋转.已知连接杆BC的长度为20cm,BD=![]() cm,压柄与托板的长度相等.
cm,压柄与托板的长度相等.
(1)当托板与压柄的夹角∠ABC=30°时,如图①点E从A点滑动了2cm,求连接杆DE的长度.
(2)当压柄BC从(1)中的位置旋转到与底座垂直,如图②.求这个过程中,点E滑动的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握我区中考模拟数学试题的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,将随机抽取的部分学生成绩(得分为整数,满分为130分)分为5组:第一组5570;第二组7085;第三组85100;第四组100115;第五组115130,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
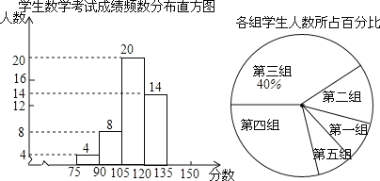
(1)本次调查共随机抽取了__ _名学生;
(2)补全频数分布直方图;
(3)将得分转化为等级,规定:得分低于70分评为“D”,70100分评为“C”,10011评为“B”,115130分评为“A”,根据目前的统计,请你估计全区该年级4500名考生中,考试成绩评为“B”级及其以上的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
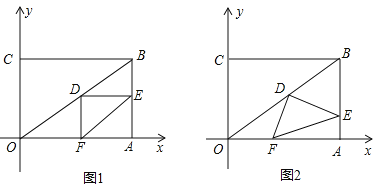
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
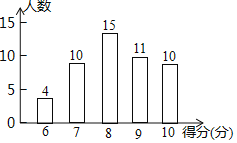
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)
请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)2+2(x﹣m)(m为常数)
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)当m取什么值时,该函数的图象关于y轴对称?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学概念
在两个等腰三角形中,如果其中一个三角形的底边长和底角的度数分别等于另一个三角形的腰长和顶角的度数,那么称这两个等腰三角形互为姊妹三角形.
概念理解
(1)如图①,在△ABC中,AB=AC,请用直尺和圆规作出它的姊妹三角形(保留作图痕迹,不写作法).
特例分析
(2)①在△ABC中,AB=AC,∠A=30°,![]() ,求它的姊妹三角形的顶角的度数和腰长;
,求它的姊妹三角形的顶角的度数和腰长;
②如图②,在△ABC中,AB=AC,D是AC上一点,连接BD.若△ABC与△ABD互为姊妹三角形,且△ABC∽△BCD,则∠A= °.
深入研究
(3)下列关于姊妹三角形的结论:
①每一个等腰三角形都有姊妹三角形;
②等腰三角形的姊妹三角形是锐角三角形;
③如果两个等腰三角形互为姊妹三角形,那么这两个三角形可能全等;
④如果一个等腰三角形存在两个不同的姊妹三角形,那么这两个三角形也一定互为姊妹三角形.
其中所有正确结论的序号是 .
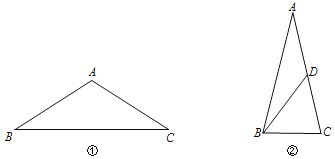
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )

A. 54°B. 64°C. 74°D. 26°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,垂直于x轴的直线l分别于函数y=x-a+1和y+x2-2ax的图像相交于P,Q两点.若平移直线l,可以使P,Q都在x轴的下方,则实数a的取值范围是_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com