
【题目】如图1,AB是⊙O的直径,过⊙O上一点C作直线l,AD⊥l于点D.
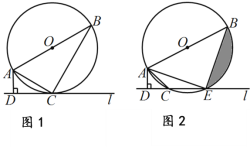
(1)连接AC、BC,若∠DAC=∠BAC,求证:直线l是⊙O的切线;
(2)将图1的直线l向上平移,使得直线l与⊙O交于C、E两点,连接AC、AE、BE, 得到图2. 若∠DAC=45°,AD=2cm,CE=4cm,求图2中阴影部分(弓形)的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)B(-1,-2)两点,与![]() 轴相交于点C.
轴相交于点C.
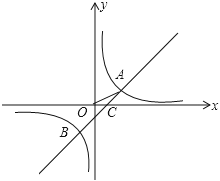
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
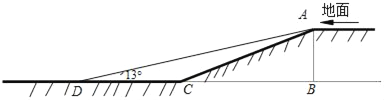
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
查看答案和解析>>
科目:初中数学 来源: 题型:
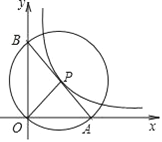
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张画有内切圆⊙P的直角三角形纸片AOB置于平面直角坐标系中,已知点A(0,3),B(4,0),⊙P与三角形各边相切的切点分别为D、E、F. 将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转,第一次旋转至图①位置,第二次旋转至图②位置,…,则直角三角形纸片旋转2018次后,它的内切圆圆心P的坐标为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
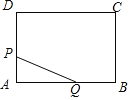
A.  B.
B. 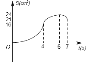 C.
C. 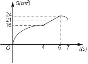 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=![]() ,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
(1)求半径OB的长;
(2)如果点P是弧AB的中点,联结PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP、CA交于点D,求线段DP的长.
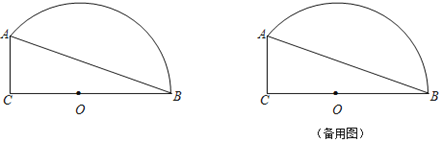
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线OE的对称点,是否存在点
关于直线OE的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 上?若存在,请直接写出相应的点
上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com