练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

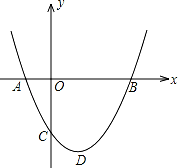
    如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1，3．与y轴负半轴交于点C，在下面五个结论中：

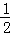    ①2a﹣b=0；②a+b+c＞0；③c=﹣3a；④只有当a=时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a值可以有四个．

    其中正确的结论是　　．（只填序号）

     


    ③④


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    一个直角三角形的斜边长为8，内切圆半径为1，则这个三角形的周长等于      (    )

     A．21     B．20 　　C．19      D．18

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，是某公园的一角，∠AOB=90°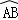，的半径OA长是6米，点C是OA的中点，点D在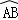上，CD∥OB，则图中草坪区（阴影部分）的面积是（　　）

    　

    A．

    （3π+）米

    B．

    （π+）米

    C．

    （3π+9）米

    D．

    （π﹣9）米

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y＝ax2+bx+c的图象向下平移1个单位长度，再向左平移2个单位长度，所得新抛物线的解析式为y＝－3x2，则a+b+c等于    (    )

        A．－3    B.- 2    C．2    D．±2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y＝ax2+bx+c的图象经过点(2，5)，(－2，－3)，(1，0)，则该二次函数的解析式为    ．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图2 - 147所示，在边长为a的等边三角形ABC中作内接矩形EFGH，使F，G在BC边上，E，H分别在AB，AC边上，求这个矩形的面积S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3－202所示，CD是⊙O的直径，A，B是⊙O上的两点．若∠ABD＝20°，则∠ADC的度数为    (    )

      　　A．40°   　　　B．50°  　　 C．60°  　　　　D．70°

    　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


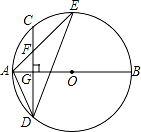
    如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足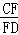=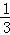，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．

    （1）求证：△ADF∽△AED；

    （2）求FG的长；

    （3）求证：tan∠E=．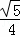

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    要使(ax2-3x)(x2-2x-1)的展开式中不含x3项,则a=　　　　.

    查看答案和解析>>

    同步练习册答案