Question

14．同圆中，内接正六边形与内接正方形的面积比是3$\sqrt{3}$：4．

Answer 1

分析 将圆内接正四边形和圆内接正六边形的边长用圆的半径表示出来，再求出圆内接正四边形与正六边形的面积表达式（用圆的半径表示），然后即可得出其面积比．

解答 解：设圆的半径为r．如图：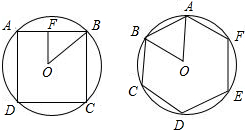
在正方形ABCD中，作边心距OF，
则OF=OBsin45°=$\frac{\sqrt{2}}{2}$r，
则AD=2×$\frac{\sqrt{2}}{2}$r=$\sqrt{2}$r，
圆内接正四边形的面积为S_ABCD=（$\sqrt{2}$r）²=2r²；
在正六边形ABCDEF中，
AB=BO=OA=r，
则S_ABCDEF=6×$\frac{1}{2}$OA•OBsin60°，
=6×$\frac{1}{2}$r•rsin60°，
=6×$\frac{\sqrt{3}}{4}$r²，
=$\frac{3\sqrt{3}}{2}$r²，
S_ABCDEF：S_ABCD=$\frac{3\sqrt{3}}{2}$r²：2r²=3$\sqrt{3}$：4；
故答案为：3$\sqrt{3}$：4．

点评 此题主要考查正多边形的计算问题，属于常规题．解答时要熟悉正方形和正六边形的面积计算方法，尤其要懂得分割计算再求和．