【题目】（1）如图①，在四边形
中，
，点
是
的中点，若
是
的平分线，试判断
，
，
之间的等量关系．
解决此问题可以用如下方法：延长交的延长线于点
，易证
得到
，从而把，，转化在一个三角形中即可判断．
，，之间的等量关系________；
（2）问题探究：如图②，在四边形中，，
与的延长线交于点，点是的中点，若是
的平分线，试探究，，
之间的等量关系，并证明你的结论．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】阅读下面的材料，解决问题.
例题:若m2 +2mn+2n2-6n+9=0,求m和n的值.
解:∵ m2+2mn+2n2- 6n+9=0,
∴m2 +2mn+n2+n2-6n+9=0,
∴(m+n)2 +(n-3)2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
问题: （1）若2x2 +4x-2xy+y2 +4=0,求xy的值;
（2）已知a, b, c是△ABC的三边长，且满足a2+b2=10a+8b-41，求c的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若△ABC的三边分别为a，b，c，其中a，b满足
+（b﹣8）2＝0．
（1）求边长c的取值范围，
（2）若△ABC是直角三角形，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①是我国古代数学家杨辉最早发现的，称为“杨辉三角”．它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！
如图②是（a+b）n的三个展开式．结合上述两图之间的规律解题：
（1）请直接写出（a+b）4的展开式：（a+b）4＝ ．
（2）请结合图②中的展开式计算下面的式：（x+2）3＝ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如今，旅游度假成为了中国人庆祝传统春节的一项的“新年俗”，山西省旅发委发布的《2018年“春节”假日旅游市场总结分析报告》中称：山西春节旅游供需两旺，实现了“旅游接待”与“经济效益”的双丰收，请根据图表信息解决问题：
（1）如图1所示，山西近五年春节假日接待海内外游客的数量逐年增加，2018年首次突破了“千万”大关，达到 万人次，比2017年春节假日增加 万人次．
（2）2018年2月15日﹣20日期间，山西省35个重点景区每日接待游客数量如下：
日期 | 2月15日 （除夕） | 2月16日 （初一） | 2月17日 （初二） | 2月18日（初三） | 2月19日 （初四） | 2月20日 （初五） |
日接待游客数量（万人次） | 7.56 | 82.83 | 119.51 | 84.38 | 103.2 | 151.55 |
这组数据的中位数是 万人次．
（3）根据图2中的信息预估：2019年春节假日山西旅游总收入比2018年同期增长的百分率约为 ，理由是 ．
（4）春节期间，小明在“青龙古镇第一届新春庙会”上购买了A，B，C，D四枚书签（除图案外完全相同）．正面分别印有“剪纸艺术”、“国粹京剧”、“陶瓷艺术”、“皮影戏”的图案（如图3），他将书签背面朝上放在桌面上，从中随机挑选两枚送给好朋友，求送给好朋友的两枚书签中恰好有“剪纸艺术”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，过边长为3的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
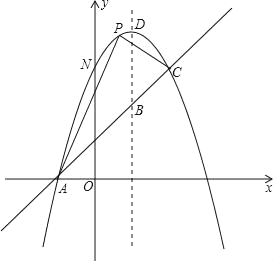
【题目】如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0）、C（2，3）两点，与y轴交于点N，其顶点为D．
（1）求抛物线及直线AC的函数关系式；
（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；
（3）设点M（3，n），求使MN+MD取最小值时n的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
