
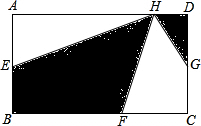
 如图所示,长方形ABCD中,AE=EB,BC=3BF,CG=GD,H是AD上任意一点,则图中阴影部分的面积是长方形ABCD的几分之几?
如图所示,长方形ABCD中,AE=EB,BC=3BF,CG=GD,H是AD上任意一点,则图中阴影部分的面积是长方形ABCD的几分之几? 分析 由题意得出△AEH和△BEH的面积相等;△CGH和△DGH的面积相等;△BFH的面积=$\frac{1}{3}$△BCH的面积=$\frac{1}{6}$长方形ABCD的面积;即可得出阴影部分面积与长方形ABCD的面积的比.
解答 解:连接BH、CH,如图所示,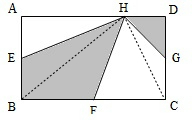
∵AE=EB,
∴△AEH和△BEH的面积相等;
∵CG=GD,
∴△CGH和△DGH的面积相等;
∴△BEH的面积+△DGH的面积=$\frac{1}{4}$长方形ABCD的面积,
∵BC=3BF,
∴△BFH的面积=$\frac{1}{3}$△BCH的面积=$\frac{1}{6}$长方形ABCD的面积;
∴阴影部分面积=($\frac{1}{6}$+$\frac{1}{4}$)长方形ABCD的面积;
∴阴影部分面积:长方形ABCD的面积=($\frac{1}{6}+\frac{1}{4}$):1=$\frac{5}{12}$;
即图中阴影部分的面积是长方形ABCD的$\frac{5}{12}$.
点评 本题考查了矩形的性质、三角形和矩形面积的计算;熟练掌握矩形的性质和三角形的面积关系是解决问题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
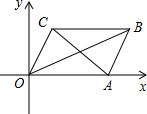 如图,在平面直角坐标系xOy中,A(4,0),OA=OC,∠AOC=60°,且CB∥OA,OB平分∠AOC,点P是四边形OABC的内部一点,且点P到四边形OABC四条边的距离相等.
如图,在平面直角坐标系xOy中,A(4,0),OA=OC,∠AOC=60°,且CB∥OA,OB平分∠AOC,点P是四边形OABC的内部一点,且点P到四边形OABC四条边的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
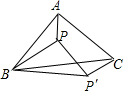 如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.
如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a2-a2=2 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | ($\sqrt{5}$)2=25 | D. | $\sqrt{(-1)^{2}}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com