
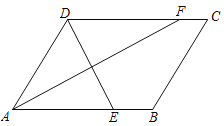
【题目】如图,平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点F,
于点F,![]() ,交
,交![]() 点
点![]() ,
,![]() ,则
,则![]() =_________.
=_________.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
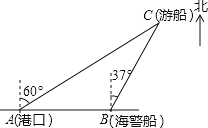
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:直线AB:y=﹣3x+3与两坐标轴交于A,B两点.
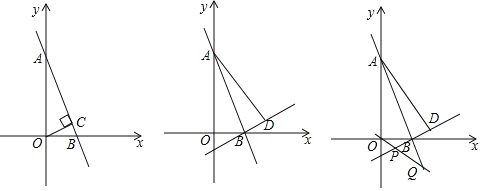
(1)过点O作OC⊥AB于点C,求OC的长;
(2)将△AOB沿AB翻折到△ABD,点O与点D对应,求直线BD的解析式;
(3)在(2)的条件下,正比例函数y=kx与直线BD交于P,直线AB交于Q,若OP=3OQ,求正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(a,4)(其中a<-3),射线OA与反比例函数![]() 的图象交于点P,点B,C分别在函数
的图象交于点P,点B,C分别在函数![]() 的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
(1)当a=-6,求线段AC的长;
(2)当AB=BO时,求点A的坐标;
(3)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
某同学在计算3(4+1)(42+1)时,发现把3写成4-1后,可以连续运用平方差公式计算,
3(4+1)(42+1)
=(4-1)(4+1)(42+1)
=(42-1)(42+1)
=44-1
=256-1
=255.
请借鉴该同学的经验,计算下列各式的值:
(1)(2+1)(22+1)(24+1)(28+1)…(22019+1)
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 是菱形,点
是菱形,点![]() 分别在
分别在![]() 上,且
上,且![]() ,点
,点![]() 分别在
分别在![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() .
.
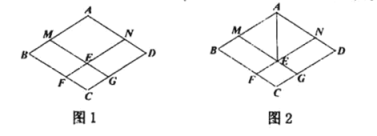
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,连接![]() ,在不添加任何辅助线的情况下,请直接写出面积相等的四边形
,在不添加任何辅助线的情况下,请直接写出面积相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
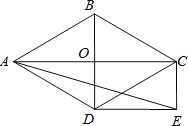
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com