
【题目】已知四边形![]() 是菱形,点
是菱形,点![]() 分别在
分别在![]() 上,且
上,且![]() ,点
,点![]() 分别在
分别在![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() .
.
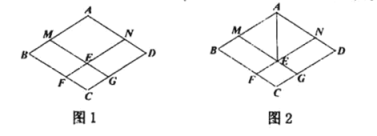
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,连接![]() ,在不添加任何辅助线的情况下,请直接写出面积相等的四边形
,在不添加任何辅助线的情况下,请直接写出面积相等的四边形
【答案】(1)见解析;(2)四边形MBFE与四边形DNEG,四边形MBCG与四边形DNFC,四边形ABFE与四边形ADGE,四边形ABFN与四边形ADGM.
【解析】
(1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)根据四边形AMEN是菱形得到ME=NE,S△AEM=S△AEN,作出辅助线,证明△MHB≌△NKD(AAS),得到MH=NK,从而得到S四边形MBFE=S四边形DNEG,继而求得答案.
(1)证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∵四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴ABBM=ADDN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)解:∵四边形AMEN是菱形,
∴ME=NE,∴S△AEM=S△AEN,
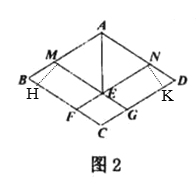
如图所示,过点M作MH⊥BC于点H,过点N作NK⊥CD于点K,
∴∠MHB=∠NKD=90°
∵四边形ABCD是菱形,
∴∠B=∠D,
∵BM=DN,
∴△MHB≌△NKD(AAS),
∴MH=NK
∴S四边形MBFE=S四边形DNEG,
∴S四边形MBCG=S四边形DNFC,S四边形ABFE=S四边形ADGE,S四边形ABFN=S四边形ADGM.
∴面积相等的四边形有:四边形MBFE与四边形DNEG,四边形MBCG与四边形DNFC,四边形ABFE与四边形ADGE,四边形ABFN与四边形ADGM.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
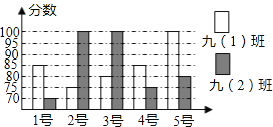
【题目】我区某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:
(1)九(1)班复赛成绩的中位数是 分,九(2)班复赛成绩的众数是 分;
(2)小明同学已经算出了九(1)班复赛的平均成绩![]() =85分;方差S2=
=85分;方差S2=![]() [(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
(3)根据(2)中计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
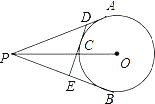
【题目】如图,PA、PB切⊙O于A.B,点C在AB上,DE切⊙O于C,交PA、PB于D.E,已知PO=5cm,⊙O的半径为3cm,则△PDE的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上一点,
上一点,![]() ,点
,点![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,
,![]() 的面积为48.
的面积为48.
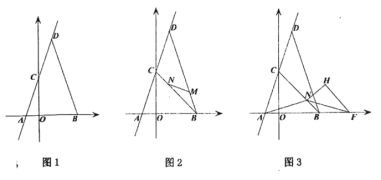
(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,连接
上,连接![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,如图3,连接![]() ,点
,点![]() 为
为![]() 轴正半轴上点
轴正半轴上点![]() 右侧一点,点
右侧一点,点![]() 为第一象限内一点,
为第一象限内一点,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,直线
上一点,直线![]() 经过点
经过点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,请你判断四边形
,请你判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋中有3张形状大小完全相同的卡片,编号为1、2、3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率;
(3)任选一个符合(2)题条件的方程,设此方程的两根为x1、x2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
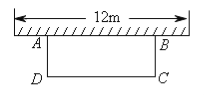
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com