
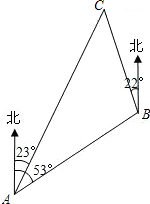
 我国海监船巡航编队从钓鱼岛(A点出发),沿北偏东53°的方向航行,航行一段时间到达一个灯塔(B点)后,又沿着北偏西22°方向航行了10海里到达黄尾屿(C点)处,这时从钓鱼岛测得巡航编队在钓鱼岛北偏东23°方向上,求钓鱼岛与黄尾屿之间的距离(参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7,结果保留整数)
我国海监船巡航编队从钓鱼岛(A点出发),沿北偏东53°的方向航行,航行一段时间到达一个灯塔(B点)后,又沿着北偏西22°方向航行了10海里到达黄尾屿(C点)处,这时从钓鱼岛测得巡航编队在钓鱼岛北偏东23°方向上,求钓鱼岛与黄尾屿之间的距离(参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7,结果保留整数) 分析 根据题意先求出∠C的度数,再过点B作BD⊥AC,垂足为D,则CD=BD,根据余弦的定义求出CD,再根据正切的定义求出AD,然后根据AC=AD+CD,即可得出答案.
解答 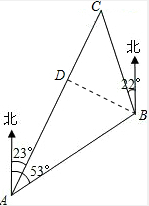 解:∵∠BAC=53°-23°=30°,
解:∵∠BAC=53°-23°=30°,
∴∠C=23°+22°=45°,
过点B作BD⊥AC,垂足为D,则CD=BD,
∵BC=10,
∴CD=BC×cos45°=5$\sqrt{2}$≈7.0,
∴AD=$\frac{BD}{{tan{{30}^0}}}$=$5\sqrt{2}×\sqrt{3}$=5×1.4×1.7≈11.9,
∴AC=AD+CD=11.9+7.0=18.9≈19(海里),
答:钓鱼岛与黄尾屿之间的距离是19海里.
点评 此题考查了解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
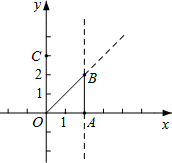 抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).
抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
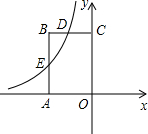 如图,矩形OABC的顶点A,C分别在x轴和y轴上,若OA=4,OC=6,写出一个函数y=$\frac{k}{x}({k≠0})$,使它的图象与矩形OABC的两边AB,BC分别交于点D,E,这个函数的表达式为y=-$\frac{1}{x}$.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,若OA=4,OC=6,写出一个函数y=$\frac{k}{x}({k≠0})$,使它的图象与矩形OABC的两边AB,BC分别交于点D,E,这个函数的表达式为y=-$\frac{1}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
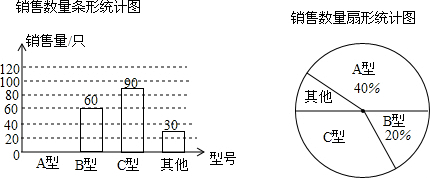
| A型 | B型 | C型 | |
| 进价(元/只) | 50 | 30 | 20 |
| 售价(元/只) | 70 | 45 | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com