
���� ��1���Ƚ�x2-1��-2�Ĵ�С���õ��𰸣�
��2����x2-2x+k��Ϊ��x-1��2+k-1����ʽ��ȷ��k��ȡֵ��Χ��
��3�����ݵ�-2��x��3ʱ��y=x2-2x-15��ֵС��y=m��x+1����ֵ����ɣ�
��� �⣺��1����x2��0��
��x2-1��-1��
��x2-1��-2��
��min{x2-1��-2}=-2��
��2����x2-2x+k=��x-1��2+k-1��
�ࣨx-1��2+k-1��k-1��
��min{x2-2x+k��-3}=-3��
��k-1��-3��
��k��-2��
��3������y=x2-2x-15����x=-2ʱ��y=-7��
��x=3ʱ��y=-12��
�������֪������y=x2-2x-15��ֱ��y=m��x+1���Ľ�������Ϊ��-2��-7������3��-12����
����m�ķ�Χ�ǣ�-3��m��7��
���� ���⿼���������κ�����һ�κ����йص��¶��壬�������������¶���ļ��㹫ʽ�ǽ���Ĺؼ���ע�⣺һ�κ����Ͷ��κ��������ʵ����ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
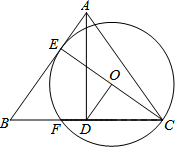 ��ͼ���ڡ�ABC�У�AB=AC��AD��BC�ڵ�D������C����O���AB�����ڵ�E����BC�ڵ�F��CEΪ��O��ֱ����
��ͼ���ڡ�ABC�У�AB=AC��AD��BC�ڵ�D������C����O���AB�����ڵ�E����BC�ڵ�F��CEΪ��O��ֱ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
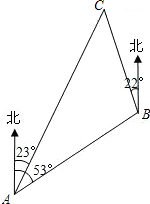 �ҹ����ബѲ����Ӵӵ��㵺��A����������ر�ƫ��53��ķ����У�����һ��ʱ�䵽��һ��������B�㣩�������ű�ƫ��22�㷽������10���ﵽ���β�죨C�㣩������ʱ�ӵ��㵺���Ѳ������ڵ��㵺��ƫ��23�㷽���ϣ�����㵺���β��֮��ľ��루�ο����ݣ�$\sqrt{2}��$1.4��$\sqrt{3}$��1.7���������������
�ҹ����ബѲ����Ӵӵ��㵺��A����������ر�ƫ��53��ķ����У�����һ��ʱ�䵽��һ��������B�㣩�������ű�ƫ��22�㷽������10���ﵽ���β�죨C�㣩������ʱ�ӵ��㵺���Ѳ������ڵ��㵺��ƫ��23�㷽���ϣ�����㵺���β��֮��ľ��루�ο����ݣ�$\sqrt{2}��$1.4��$\sqrt{3}$��1.7����������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ס�����ר����ij��ʱ������������y��Ԫ��������x���죩�ĺ���ͼ����ͼ��ʾ�������ڼ���ר����ͣҵװ��һ��ʱ�䣬���¿�ҵ����ר������վ�����������ԭ����2���������������⣺
�ס�����ר����ij��ʱ������������y��Ԫ��������x���죩�ĺ���ͼ����ͼ��ʾ�������ڼ���ר����ͣҵװ��һ��ʱ�䣬���¿�ҵ����ר������վ�����������ԭ����2���������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
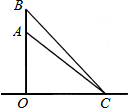 ��ͼ��һֻ���������ɵ�A�����ӵ���C���AC�ľ�����6m��������43�㣬1s����������B������ʱ���BC�ľ�����6.13m������Ϊ45.54�㣬�����������
��ͼ��һֻ���������ɵ�A�����ӵ���C���AC�ľ�����6m��������43�㣬1s����������B������ʱ���BC�ľ�����6.13m������Ϊ45.54�㣬������������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com