
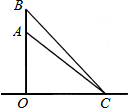
 如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题
如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题分析 (1)在Rt△BOC中,根据$\frac{BO}{BC}$=sin∠BCO,求出BO的长即可;
(2)在Rt△AOC中,根据$\frac{AO}{AC}$=sin∠ACO,求出AO的长,然后根据AB=BO-AO,求出AB的长,从而可知A点跳到B点的平均速度.
解答 解:(1)在Rt△BOC中,$\frac{BO}{BC}$=sin∠BCO,
即$\frac{BO}{6.13}$=sin45.54°,
解得,BO≈0.714×6.13≈4.38米.
(2)在Rt△AOC中,$\frac{AO}{AC}$=sin∠ACO,
即$\frac{AO}{AC}$=sin43°,
$\frac{AO}{6}$=0.682,
解得,AO≈6×0.682≈4.092米,
AB=BO-AO=4.38-4.092=0.288米,
松鼠从A点跳到B点的平均速度是0.288÷1≈0.29米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
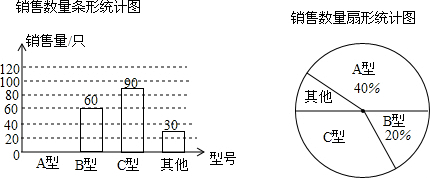
| A型 | B型 | C型 | |
| 进价(元/只) | 50 | 30 | 20 |
| 售价(元/只) | 70 | 45 | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
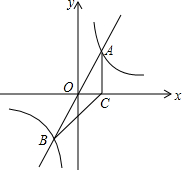 如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
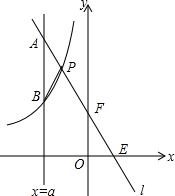 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{2}{x}$(x<0)交于点P(-1,n),且F是PE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com