
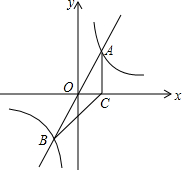
 如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.分析 (1)把A的坐标分别代入函数的解析式,即可求得k和m的值,从而求得函数解析式;
(2)根据A和B关于原点对称,求得B的坐标,则三角形的面积即可求得;
(3)mx>$\frac{k}{x}$即写出对于相同的x的值,一次函数的图象在上边的部分对应的自变量的取值范围.
解答 解:(1)把A(1,2)代入y=mx得m=2,则解析式是y=2x,
把A(1,2)代入y=$\frac{k}{x}$得:k=2,
则解析式是y=$\frac{2}{x}$;
(2)A的坐标是(1,2),则B的坐标是(-1,-2).
则S△ABC=$\frac{1}{2}$×2×4=4;
(3)根据图象可得:-1<x<0或x>1.
点评 本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.


科目:初中数学 来源: 题型:解答题
 甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图所示.在这期间乙专卖店停业装修一段时间,重新开业后,乙专卖店的日均销售收入是原来的2倍.请解决下列问题:
甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图所示.在这期间乙专卖店停业装修一段时间,重新开业后,乙专卖店的日均销售收入是原来的2倍.请解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
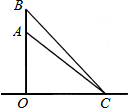 如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题
如图,一只松鼠在树干的A处,从地面C测得AC的距离是6m,仰角是43°,1s后,松鼠跳到B处,此时测得BC的距离是6.13m,仰角为45.54°,解答下列问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com