
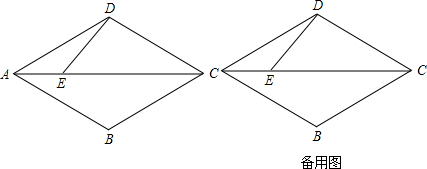
分析 (1)根据题意可以补全图形;
(2)连接BE,根据已知条件和图形可以证明△GEB≌△CBE,得到答案;
(3)根据△GEB≌△CBE,得到EC=BG,EG=BC,根据等腰三角形的性质和∠BAC=30°,求出AB和BC的关系,得到答案.
解答 解:(1)补全图形,如图1所示: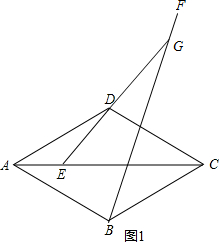
(2)证明:连接BE,如图2:
∵四边形ABCD是菱形,
∴AD∥BC,∠ADC=120°,
∴∠DCB=60°.
∵AC是菱形ABCD的对角线,
∴∠DCA=$\frac{1}{2}$∠DCB=30°,
又∠DEC=50°,∠EDC=100°,
由菱形的对称性可知,
∠EBC=100°,
∠BEC=50°,则∠GEB=100°,
∴∠GEB=∠CBE.
∵∠FBC=50°,∴∠GBE=50°,
∴∠EBG=∠BEC.
在△GEB与△CBE中,$\left\{\begin{array}{l}∠GEB=∠CBE\\ BE=EB\\∠EBG=∠BEC\end{array}\right.$
∴△GEB≌△CBE.
∴EG=BC.
(3)由(2)得,EC=BG,EG=BC,
∴AE+BG=AC,
在三角形ABC中,BA=BC,∠BAC=30°,
∴AC=$\sqrt{3}$BC,
∴AE+BG=$\sqrt{3}$EG.
点评 本题考查的是菱形的性质,根据题意证明三角形全等是解题的关键,解答时,要正确运用菱形对角线平分一组对角,灵活运用三角形全等的知识和等腰三角形的知识进行解答.


科目:初中数学 来源: 题型:填空题
 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
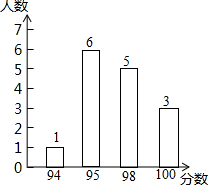 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )| A. | 98,95 | B. | 98,98 | C. | 95,98 | D. | 95,95 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
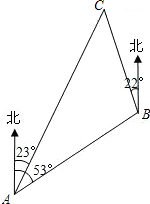 我国海监船巡航编队从钓鱼岛(A点出发),沿北偏东53°的方向航行,航行一段时间到达一个灯塔(B点)后,又沿着北偏西22°方向航行了10海里到达黄尾屿(C点)处,这时从钓鱼岛测得巡航编队在钓鱼岛北偏东23°方向上,求钓鱼岛与黄尾屿之间的距离(参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7,结果保留整数)
我国海监船巡航编队从钓鱼岛(A点出发),沿北偏东53°的方向航行,航行一段时间到达一个灯塔(B点)后,又沿着北偏西22°方向航行了10海里到达黄尾屿(C点)处,这时从钓鱼岛测得巡航编队在钓鱼岛北偏东23°方向上,求钓鱼岛与黄尾屿之间的距离(参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
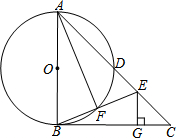 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
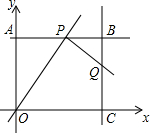 如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com