
【题目】随着我省“大美青海,美丽夏都”影响力的扩大,越来越多的游客慕名而来。根据青海省旅游局《2015年国庆长假出游趋势报告》绘制了如下尚不完整的统计图。
根据以上信息解答下列问题:
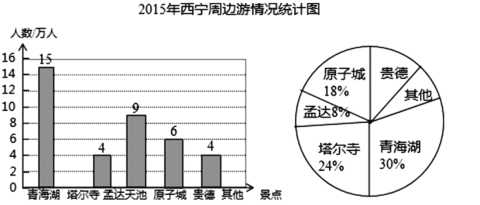
(1)2015年国庆期间,西宁周边景区共接待游客___万人,扇形统计图中“青海湖”所对应的圆心角的度数是___,并补全条形统计图;
(2)甲乙两个旅行团在青海湖、塔尔寺、原子城三个景点中,同时选择去同一个景点的概率是多少?请用画树状图或列表法加以说明,并列举所有等可能的结果。
【答案】(1)共接待游客人数为50万人,“青海湖”所对应的圆心角的度数是108°,补全条形统计图如图,见解析;(2)同时选择去同一个景点的概率是![]() .
.
【解析】
(1)根据条形图和扇形图得到游“青海湖”的人数和所占的百分比,计算出共接待游客人数,根据“青海湖”所占的百分比求出圆心角,求出塔尔寺人数,补全条形统计图;
(3)列表求出共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种,根据概率公式计算即可
(1)由条形图和扇形图可知,游“青海湖”的人数是15万人,占30%,
∴共接待游客人数为:15÷30%=50(万人),
“青海湖”所对应的圆心角的度数是:360°×30%=108°,
塔尔寺人数为:24%×50=12(万人),补全条形统计图如图:

(2) 设A,B,C分别表示青海湖、塔尔寺、原子城.列表如下:
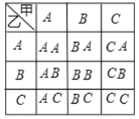
由此可见,共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种.
∴同时选择去同一个景点的概率是![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J. Nplcr,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若![]() ,那么
,那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作:
的对数,记作:![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .
.
我们根据对数的定义可得到对数的一个性质:![]() ;理由如下:
;理由如下:
设![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,由对数的定义得
,由对数的定义得![]()
又∵![]()
∴![]()
解决以下问题:
(1)将指数![]() 转化为对数式______;
转化为对数式______;
(2)证明![]()
(3)拓展运用:计算![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
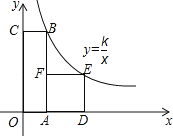
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=![]() 的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边![]() 的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线
的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线![]() 是经过点P的一条直线,把
是经过点P的一条直线,把![]() 沿直线
沿直线![]() 折叠,点B的对应点是点
折叠,点B的对应点是点![]() .
.
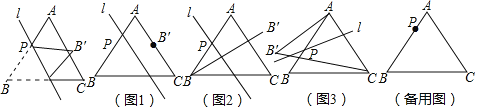
(1)如图1,当![]() 时,若点
时,若点![]() 恰好在AC边上,则
恰好在AC边上,则![]() 的长度为 ;
的长度为 ;
(2)如图2,当![]() 时,若直线
时,若直线![]() ,则
,则![]() 的长度为 ;
的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线![]() 始终垂直于AC,
始终垂直于AC,![]() 的面积是否变化?若变化,说明理由;若不变化,求出面积;
的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当![]() 时,在直线
时,在直线![]() 变化过程中,求
变化过程中,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知菱形ABCD的边长为2![]() ,点A在x轴负半轴上,点B在坐标原点。点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点。点D的坐标为(![]() ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
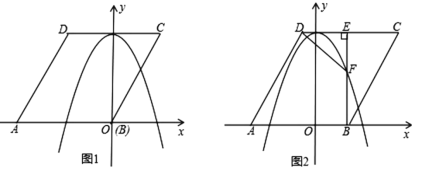
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF.设菱形ABCD平移的时间为t秒(0<t<3)
①是否存在这样的t,使DF=![]() FB?若存在,求出t的值;若不存在,请说明理由;
FB?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
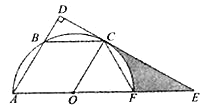
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)若半圆O的半径为12,求涂色部分的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=16,BC=12,点D、E分别为边AB、BC中点,点P从点A出发,沿射线AB方向以每秒5个单位长度的速度向点B运动,到点B停止.当点P不与点A重合时,过点P作PQ∥AC,且点Q在直线AB左侧,AP=PQ,过点Q作QM⊥AB交射线AB于点M.设点P运动的时间为t(秒)
(1)用含t的代数式表示线段DM的长度;
(2)求当点Q落在BC边上时t的值;
(3)设△PQM与△DEB重叠部分图形的面积为S(平方单位),当△PQM与△DEB有重叠且重叠部分图形是三角形时,求S与t的函数关系式;
(4)当经过点C和△PQM中一个顶点的直线平分△PQM的内角时,直接写出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:①将半径2的⊙O六等分,依次得到A,B,C,D,E,F六个分点; ②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案是_________
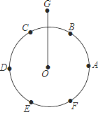
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com