
【题目】如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE.
(1)求证:DE是⊙O的切线;
(2)若CD=![]() ,∠ACB=30°,求OE的长.
,∠ACB=30°,求OE的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD、BD,OD||BC,DE⊥BC,所以DE⊥OD.
(2)利用30°的特殊三角形求出DE长,再利用勾股定理得到OE长.
试题解析:
(1)证明:连接OD、BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴D为AC中点,
∵OA=OB,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O的切线;
(2)解:∵CD=![]() ,∠ACB=30°,
,∠ACB=30°,
∴BC=2,
∴BD=![]() BC=1,
BC=1,
∵AB=BC,
∴∠A=∠C=30°,
∵BD=1,
∴AB=2BD=2,
∴OD=1,
在Rt△CDB中,由三角形面积公式得:BC×DE=BD×CD,
1×![]() =2DE,
=2DE,
DE=![]() ,在Rt△ODE中,由勾股定理得:OE=
,在Rt△ODE中,由勾股定理得:OE=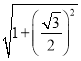 =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
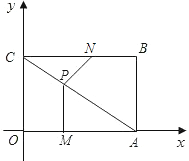
【题目】如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了![]() 秒.
秒.
(1)当![]() 时,求PC的长;
时,求PC的长;
(2)当![]() 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的角平分线
的角平分线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() .
.


(1)求直线![]() 的解析式;
的解析式;
(2)如图2,若点![]() 为直线
为直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,当四边形
,当四边形![]() 为菱形时,求
为菱形时,求![]() 的面积;
的面积;
(3)如图3,点![]() 为
为![]() 轴上的一个动点,连接
轴上的一个动点,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,当以点
,当以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形时,求点
为顶点的三角形是等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
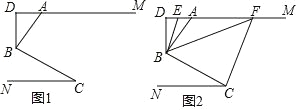
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示.

(1)若该商场计划购进两种多媒体教学设备若干套,共需124万元,全部销售后可获毛利润36万元.则该商场计划购进A,B两种品牌的多媒体教学设备各多少套?
(2)通过市场调研,该商场决定在(1)中所购总数量不变的基础上,减少A种设备的购进数量,增加B种设备的购进数量.若用于购进这两种多媒体教学设备的总资金不超过120万元,且全部销售后可获毛利润不少于33.6万元.问有几种购买方案?并写出购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com