
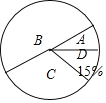
����Ŀ��ij�н���չ�ݽ��������ijУ�Բμ�ѡ�ε�ѧ���ijɼ���A��B��C��D�ĸ��ȼ�����ͳ�ƣ����������²�������ͳ�Ʊ�������ͳ��ͼ��
�ɼ��ȼ� | Ƶ�� | Ƶ�� |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
��1����m��n��ֵ��
��2������C�ȼ�������Ӧ������Բ�ĽǵĶ�����
��3����֪�ɼ��ȼ�ΪA��4��ѧ������1��������3��Ů�����ִ��������ѡ2��ѧ������ѧУ�μ�ȫ�б��������ǡ��ѡ��һ������һŮ���ĸ���
���𰸡���1��m��51��������n��0.04����2��108������3��![]()
��������
��1������������������ٸ���Ƶ��=Ƶ�����������ɵô𰸣�
��2�������C�ȼ�����������360������C�ȼ�������ռ�������ɵã�
��3���б��ó����еȿ��ܵ���������ҳ��պó鵽һ��һŮ��������������������ĸ��ʣ�
�⣺��1������������Ϊ15��15%��100��������
��m��100��0.51��51��������n��4��100��0.04��
��2��C�ȼ�����Ϊ100��4��51��15��30��������
����C�ȼ�������Ӧ������Բ�ĽǵĶ���Ϊ360���![]() ��108����
��108����
��3���б����£�
�� | Ů1 | Ů2 | Ů3 | |
�� | ������ | ��Ů���У� | ��Ů���У� | ��Ů���У� |
Ů1 | ���У�Ů�� | ������ | ��Ů��Ů�� | ��Ů��Ů�� |
Ů2 | ���У�Ů�� | ��Ů��Ů�� | ������ | ��Ů��Ů�� |
Ů3 | ���У�Ů�� | ��Ů��Ů�� | ��Ů��Ů�� | ������ |
�߹���12�ֵȿ��ܵĽ����ѡ��1��������1��Ů���������6�֣�
��P��ѡ��1��������1��Ů������![]() ��
��


 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
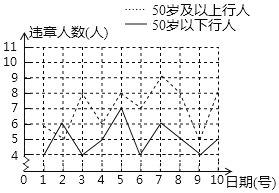
����Ŀ��Ϊ����ȫ���������еĴ������������н�������10���ij·��100����50��������������100����50�꼰�����������г��ֽ�ͨΥ�µ���������˵���ͳ�ƣ����������ݻ��Ƴ�����ͳ��ͼ�������������Ϣ�������������
(1)����10����50�꼰������������ÿ��Υ��������������
(2)ij�������°�ʱ�ξ�����һ·�ڵ���50������������Ϊ300�ˣ�����ƴ�Լ�ж����˻���ֽ�ͨΥ����Ϊ��
(3)��ѡ���ʵ���ͳ����������50����������������50��������������ͨΥ����Ϊ���ֲ������������д������ٽ�ͨΥ��������������飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
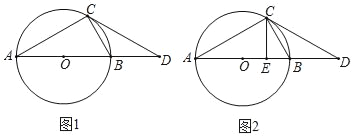
����Ŀ����֪����ͼ����O�������뾶OA��OB��C��D��![]() �����ȷֵ㣬OC��OD�ֱ���AB�ཻ�ڵ�E��F��
�����ȷֵ㣬OC��OD�ֱ���AB�ཻ�ڵ�E��F��
��֤��CD��AE��BF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ뾶Ϊ4����O��ֱ����P��Բ������A��B������һ�㣬��APB��ƽ���߽���O�ڵ� C������AC��BC����ABC����λ�����ڵ�ֱ������O�ཻ�ڵ�E��F����EF�ij���________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�Ĵ�ʡ�Ű��У���ͼ���ı���ABCD�У�AB=4��BC=6��AB��BC��BC��CD��EΪAD���е㣬FΪ�߶�BE�ϵĵ㣬��FE=![]() BE�����F����CD�ľ����� ��������
BE�����F����CD�ľ����� ��������

A. 3 B. ![]() C. 4 D.
C. 4 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B����ֱ�λ��һ�����������ˣ�����������������ֱ�Ӳ���A��B��ľ���.С������ѧ����֪ʶ��������������ֲ�����������ͼ�١��ڡ�����ʾ��ͼ��a��b��c��ʾ���ȣ�.
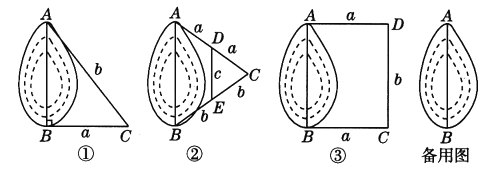
��1������д��С����Ƶ����ֲ���������AB�ij��ȣ�
ͼ���У�AB=______��ͼ���У�AB=______��ͼ���У�AB=______��
��2�����������һ�ֲ�ͬ���������ֵIJ�������������ʾ��ͼ����Ҫ��д������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�У���B��30�㣬��ACB��90�㣬�ӳ�CA��O��ʹAO��AC����OΪԲ�ģ�OA��Ϊ�뾶����O��BA�ӳ����ڵ�D������CD��
��1����֤��CD����O�����ߣ�
��2����AB��4����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ݹ�˾ÿ������9��00��10��00Ϊ�����������ɼ�ʱ�Σ��ײֿ��������տ�����Ҳֿ������ɷ��������ʱ���ڼף������ֿ�Ŀ������![]() ��������ʱ��
��������ʱ��![]() ���֣�֮��ĺ���ͼ����ͼ��ʾ����ô�����ֿ��ݼ�����ͬʱ���˿̵�ʱ��Ϊ�� ��
���֣�֮��ĺ���ͼ����ͼ��ʾ����ô�����ֿ��ݼ�����ͬʱ���˿̵�ʱ��Ϊ�� ��

A. 9��15B. 9��20C. 9��25D. 9��30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1�����ڡ�ABC�У���ACB=90������ABΪֱ������O������C��ֱ��CD��AB���ӳ����ڵ�D����BD=OB��CD=CA��
��1����֤��CD�ǡ�O�����ߣ�
��2����ͼ��2��������C��CE��AB�ڵ�E������O�İ뾶Ϊ8����A=30�������߶�BE��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com