
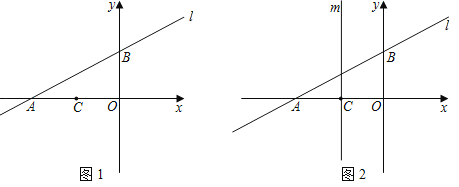
【题目】如图1,直线l:y=![]() x+2与x轴交于点A,与y轴交于点B.已知点C(﹣2,0).
x+2与x轴交于点A,与y轴交于点B.已知点C(﹣2,0).
(1)求出点A,点B的坐标.
(2)P是直线AB上一动点,且△BOP和△COP的面积相等,求点P坐标.
(3)如图2,平移直线l,分别交x轴,y轴于交于点A1,B1,过点C作平行于y轴的直线m,在直线m上是否存在点Q,使得△A1B1Q是等腰直角三角形?若存在,请直接写出所有符合条件的点Q的坐标.
【答案】(1)点A的坐标为(﹣4,0),点B的坐标的坐标为(0,2);(2)点P坐标为(4,4);(3)点Q为(﹣2,2)或(﹣2,﹣2)或(﹣2,-4)或(﹣2,![]() ).
).
【解析】
(1)根据求与![]() 轴交点坐标的方法,列出方程即可得到结论;
轴交点坐标的方法,列出方程即可得到结论;
(2)设![]() ,根据面积公式列出方程即可得出结论;
,根据面积公式列出方程即可得出结论;
(3)如图2,①当点![]() 是直角顶点时,根据全等三角形的性质即可得出结论;②当点
是直角顶点时,根据全等三角形的性质即可得出结论;②当点![]() 是直角顶点时,
是直角顶点时,![]() ,根据平移的性质得到直线
,根据平移的性质得到直线![]() 的解析式为
的解析式为![]() ,根据两点间的距离公式即可得到结论;③当点
,根据两点间的距离公式即可得到结论;③当点![]() 是直角顶点时,过点
是直角顶点时,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据全等三角形的性质即可得出结论.
,根据全等三角形的性质即可得出结论.
解:(1)设y=0,则![]() x+2=0,
x+2=0,
解得:x=﹣4,
设x=0,则y=2,
∴点A的坐标为(﹣4,0),点B的坐标的坐标为(0,2);
(2)∵点C(﹣2,0),点B(0,2),
∴OC=2,OB=2,
∵P是直线AB上一动点,
∴设P(m,![]() m+2),
m+2),
∵△BOP和△COP的面积相等,
∴![]() ×2|m|=
×2|m|=![]() 2×(
2×(![]() |m|+2),
|m|+2),
解得:m=±4,
当m=﹣4时,点P与点A重合,
∴点P坐标为(4,4);
(3)存在;
理由:如图1,
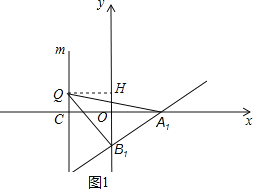
①当点B1是直角顶点时,
∴B1Q=B1A1,
∵∠A1B1O+∠QB1H=90°,∠A1B1O+∠OA1B1=90°,
∴∠OA1B1=∠QB1H,
在△A1OB1和△B1HQ中,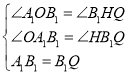 ,
,
∴△A1OB1≌△B1HQ(AAS),
∴B1H=A1O,OB1=HQ=2,
∴B1(0,﹣2)或(0,2),
当点B1(0,﹣2)时,Q(﹣2,2),
当点B1(0,2)时,
∵B(0,2),
∴点B1(0,2)(不合题意舍去),
∴Q(﹣2,2),
②当点A1是直角顶点时,A1B1=A1Q,
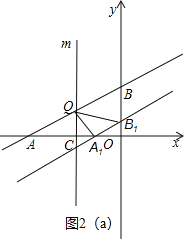
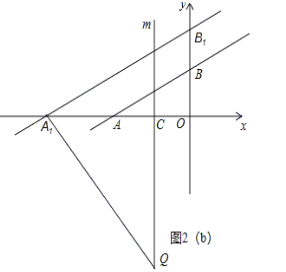
∵直线AB的解析式为y=![]() x+2,
x+2,
由平移知,直线A1B1的解析式为y=![]() x+b,
x+b,
∴A1(﹣2b,0),B1(0,b),
∴A1B12=4b2+b2=5b2,
∵A1B1⊥A1Q,
∴直线A1Q的解析式为y=﹣2x﹣4b
∴Q(﹣2,4﹣4b),
∴A1Q2=(﹣2b+2)2+(4﹣4b)2=20b2-40b+20,
∴20b2﹣40b+20=5b2,
∴b=2或b=![]() ,
,
∴Q(﹣2,-4)或(﹣2,![]() );
);
③当Q是直角顶点时,过Q作QH⊥y轴于H,

∴A1Q=B1Q,
∵∠QA1C1+∠A1QC=90°,∠A1QC+∠CQB1=90°,
∴∠QA1C=∠CQB1,
∵m∥y轴,
∴∠CQB1=∠QB1H,
∴∠QA1C=∠QB1H
在△A1QC与△B1QH中,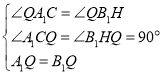 ,
,
∴△A1QC≌△B1QH(AAS),
∴CQ=QH=2,B1H=A1C,
∴Q(﹣2,2)或(﹣2,﹣2),
即:满足条件的点Q为(﹣2,2)或(﹣2,﹣2)或(﹣2,-4)或(﹣2,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】问题提出:
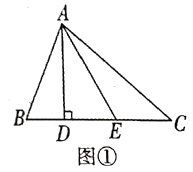
(1)如图①在![]() 中,
中,![]() 是
是![]() 边
边![]() 的高,点
的高,点![]() 是
是![]() 上任意一点,若
上任意一点,若![]() 则
则![]() 的最小值为_ ;
的最小值为_ ;
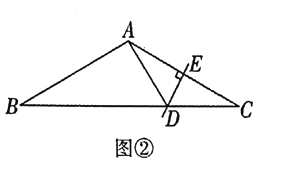
(2)如图②,在等腰![]() 中,
中,![]() 是
是![]() 的垂直平分线,分别交
的垂直平分线,分别交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
问题解决:
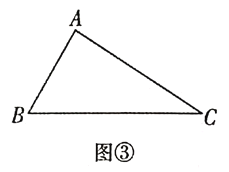
(3)如图③,某公园管理员拟在园内规划一个![]() 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路
区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路![]() 和
和![]() ,满足
,满足![]() 点
点![]() 到
到![]() 的距离为
的距离为![]() .为了节约成本,要使得
.为了节约成本,要使得![]() 之和最短,试求
之和最短,试求![]() 的最小值(路宽忽略不计).
的最小值(路宽忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数的学习中,我们经历了“确定函数表法式﹣画函数图象﹣利用函数图象研究函数性质﹣利用图象解决问题”的学习过程.在画函数图象时,我们常常通过描点或平移或翻折的方法画函数图象.小明根据学到的函数知识探究函数y1=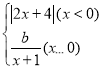 的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y1 | … | 4 | 2 | m | 2 | 4 | 2 |
| n |
| … |
(1)根据表格中x、y1的对应关系可得m=______,n=______;
(2)在平面直角坐标系中,描出表格中各点,两出该函数图象;根据函数图象,写出该函数的一条性质______.
(3)当函数y1的图象与直线y2=mx+1有三个交点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
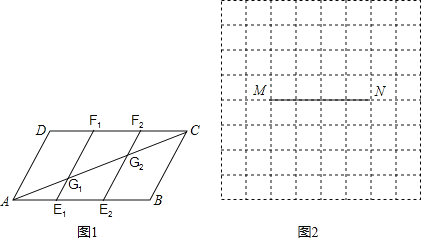
【题目】(1)如图1,在平行四边形ABCD中,点E1,E2是AB三等分点,点F1,F2是CD三等分点,E1F1,E2F2分别交AC于点G1,G2,求证:AG1=G1G2=G2C.
(2)如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“天空之城”摩天轮,位于宁波市杭州湾新区欢乐世界.摩天轮高约126米(最高点到地面的距离).如图,点O是摩天轮的圆心,AB是其垂直于地面的直径,小明在地面C处用测角仪测得摩天轮最高点A的仰角为45°,测得圆心O的仰角为30°,求摩天轮的半径.(结果保留根号)
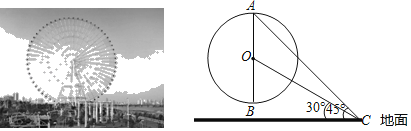
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题错误的是( ).
A.弦的垂直平分线必平分弦所对的两条弧.
B.掷一枚均匀的骰子,骰子停止转动后,2点朝上是随机事件.
C.若Rt△ABC的两边长恰为方程x2-7x+12=0的两个实数根,则其斜边长为5.
D.若直线y=ax-b与直线y=mx+n交于点(2,-1),则方程![]() 的解为
的解为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上有且只有4个点,这4个点中有一个独特的性质:连结每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.
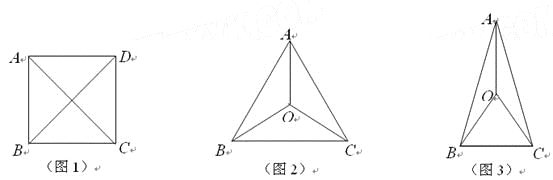
(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,接着活动学具成为图2所示,并测得∠ABC=90°,若图2对角线BD=40cm,则图1中对角线BD的长为( )
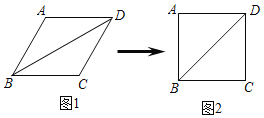
A.20cmB.20![]() cmC.20
cmC.20![]() cmD.20
cmD.20![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com