
����Ŀ����ͼ��Rt��ABC�У���ACB��90�㣬AC��6cm��BC��8cm����P�ӵ�A��������ÿ��1cm���ٶ���AC�˶���ͬʱ��Q�ӵ�C��������ÿ��2cm���ٶ���CB�˶�����Q�����Bʱ����Pͬʱֹͣ�˶���
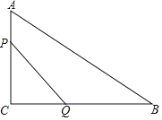
��1�����˶�����ʱ��PCQ�����Ϊ5cm2��
��2����PCQ������ܷ����10cm2�����ܣ�����˶�ʱ�䣬�����ܣ�˵�����ɣ�
��3���Ƿ����ij��ʱ��t��ʹ�ı���ABQP�������С�������ڣ�����˶�ʱ�䣬�����ܣ�˵�����ɣ�
���𰸡���1������1���PCQ���������5cm2����2�����ܣ�����������3��![]() ʱ��ʹ�ı���ABQP�������С
ʱ��ʹ�ı���ABQP�������С
��������
��1�����˶�t����PCQ���������5cm2���ֱ��ʾ���߶�CP���߶�CQ�ij��������������ε������ʽ�г�������⼴�ɣ�
��2�����������ε������ʽ�г����̣��õ��ķ�����ʵ���⣬˵����PCQ��������ܵ���10cm2��
��3����ʾ���ı���ABQP�������Ȼ�������䷽���������Сֵ���ɣ�
��1�����˶�t����PCQ���������5cm��
��������ã�
CP=6��t��QC=2t��
���PCQ������ǣ�![]() CQCP=
CQCP=![]() ��(6��t)��2t=5��
��(6��t)��2t=5��
��ã�t1=1��t2=5����ȥ����
�ʾ���1���PCQ���������5cm2��
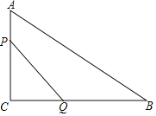
��2������PCQ������ܷ����10cm2����![]() ��(6��t)��2t=10��
��(6��t)��2t=10��
����ã�![]() ��
��
![]() ��
��
���Է�����ʵ���⣬��PCQ��������ܵ���10cm2��
��3��![]() =
=![]()
![]() ��
��
��Ϊ![]() >0��
>0��
�����ı���ABQP���������Сֵ��
��![]() ��
��
��![]() ʱ���ı���ABQP���������СֵΪ
ʱ���ı���ABQP���������СֵΪ![]() ��
��


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
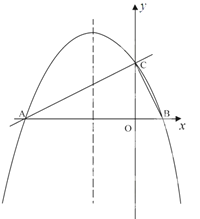
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�ֱ��![]() ��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����
��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����![]() �Ҿ���A��C���㣬��x�����һ����Ϊ��B��
�Ҿ���A��C���㣬��x�����һ����Ϊ��B��
��1����ֱ��д����B�����ꣻ���������߽���ʽ��
��2������PΪֱ��AC�Ϸ����������ϵ�һ�㣬����PA��PC�����PAC����������ֵ���������ʱ��P�����꣮
��3�����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ��������������ABC���ƣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
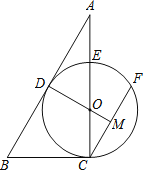
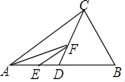
����Ŀ����ͼ���ڡ�ABC�У���O�ڱ�AC�ϣ���O���ABC�ı�BC��AB�ֱ�������C��D���㣬���AC����E�㣬��CF��ABƽ�У���DO���ӳ��߽���M�㣮
��1����֤����M��CF���е㣻
��2����E��![]() ���е㣬BC��a��
���е㣬BC��a��
����![]() �Ļ�����
�Ļ�����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�DΪб��AB���е㣬��B=60�㣬BC=2cm������E�ӵ�A������AB���B�˶�������F�ӵ�D������������D��C��B�˶���������ٶȾ�Ϊ1cm/s�������յ��ֹͣ�˶�����AE�ij�Ϊx����AEF�����Ϊy����y��x��ͼ�����Ϊ��������
A. 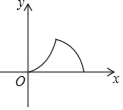 B.
B. 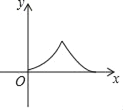
C. 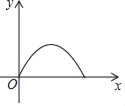 D.
D. 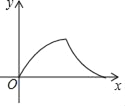
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��x+4��x�ᡢy��ֱ��ڵ�A��B��������y=��![]() ��x��m��2+n�Ķ���P��ֱ��y=��x+4�ϣ���y�ύ�ڵ�C����P��C�����B�غϣ�����BCΪ��������BCDE����CD=2����P��D��y���ͬ�࣮
��x��m��2+n�Ķ���P��ֱ��y=��x+4�ϣ���y�ύ�ڵ�C����P��C�����B�غϣ�����BCΪ��������BCDE����CD=2����P��D��y���ͬ�࣮

��1��n=________���ú�m�Ĵ���ʽ��ʾ������C����������________���ú�m�Ĵ���ʽ��ʾ����
��2������P�ھ���BCDE�ı�DE�ϣ����ڵ�һ����ʱ���������߶�Ӧ�ĺ�������ʽ��
��3��ֱ��д������BCDE����������������������ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ũ��Ҳ�ܱ���ҽ�Ʒ���!�����ǹ�����������ũ��ҽ�ƺ����ijɹ�������ֻҪÿ��ÿ�꽻10ԪǮ���Ϳ��Լ������ҽ�ƣ�ÿ�������Լ�֧��ҽ�Ʒѣ�����ʱ�ɵõ���һ���������صķ��ؿ��һ�ٴ뼫�����ǿ��ũ��������յ�������С����ͬѧ����������������һЩũ�����ռ��������ݻ��������µ�ͳ��ͼ��
����������Ϣ������������⣺
��1�����ε����� ����������Ĵ����У��� �˲μӺ���ҽ�Ƶõ��˷��ؿ�?
��2����������10000��������������ж����˲μ��˺���ҽ��?Ҫʹ�����μӺ���ҽ�Ƶ��������ӵ�9680�ˣ��������������ƽ����������ͬ������ƽ�������ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ı���ABCD�У�AB��CD����B=90����AC=AD������P�ӵ�B����������B-A-D-C������1��λ/����ٶ��˶����������˶������У���BCP�����S���˶�ʱ��t���룩�ĺ���ͼ����ͼ2��ʾ����AD���ڣ�������
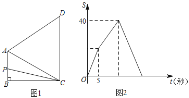
A. 10B. ![]() C. 8D.
C. 8D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ�ȵĵ���ֱ�������Σ�б�߳�Ϊ2������ͼ���ã�����һ��������45���ǵ��������һ�������ε�ֱ�Ƕ���A�غϣ���������ABC�̶�������һ���������Ƶ�A��תʱ�����ĽDZߺ�б�����ڵ�ֱ�߷ֱ����BC���ڵ�E��F����BF=![]() CE=
CE=![]() ��
��![]() ����
����![]() �ĺ���ͼ������ǣ� ��
�ĺ���ͼ������ǣ� ��
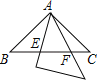
A.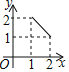 B.
B.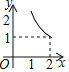 C.
C.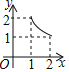 D.
D.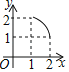
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
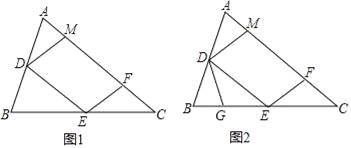
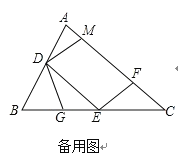
����Ŀ����ͼ1���������ABC�У�D��E�ֱ���AB��BC���е㣬��F��AC�ϣ��������AFE=��A��DM��EF��AC�ڵ�M.
��1��֤����DM=DA��
��2����ͼ2����G��BE�ϣ��ҡ�BDG=��C����֤����DEG�ס�ECF��
��3����ͼ2�У�ȡCE��һ��H��ʹ�á�CFH=��B����BG=3����EH�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com