
分析 (1)设试销时该品种苹果的进货价是每千克x元,则实际进货价为(0.5+x)元,根据这次购进苹果数量是试销时的2倍,列方程求解;
(2)设余下的苹果为y千克,求出总购进的苹果数量,根据超市在这两次苹果销售中的盈利不低于4 100元,列不等式求解.
解答 解:(1)设试销时该品种苹果的进货价是每千克x元,则实际进货价为(0.5+x)元,
由题意得,$\frac{5000}{x}$×2=$\frac{11000}{x+0.5}$,
解得:x=5,
经检验,x=5是原分式方程的解,且符合题意,
答:试销时该品种苹果的进货价是每千克5元;
(2)由(1)得,总共购进苹果:5000÷5×3=3000(kg),
设余下的苹果为y千克,
由题意得,7(3000-y)+4y-5000-11000≥4 100,
解得:y≤300.
答:余下的苹果最多为300千克.
点评 本题考查了一元一次不等式和分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 96分 | B. | 98分 | C. | 100分 | D. | 104分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
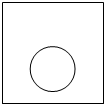 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )| A. | πr2 | B. | a2-πr2 | C. | 4r2-πr2 | D. | $\frac{a^2}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
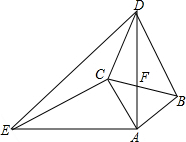 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
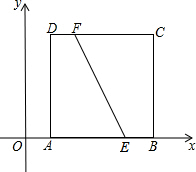 如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com