
【题目】如图,在△ABC中,D是AB的中点,E是CD的中点, 过点C作CF//AB交AE的延长线于点F,连接BF.
(1) 求证:DB=CF;
(2) 如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
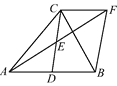
【答案】(1)证明见解析;(2)四边形BDCF是矩形,理由见解析.
【解析】试题分析:(1)根据CF∥AB,可知∠DAE=∠CFE,得出△ADE≌△FCE,再根据等量代换可知DB=CF,
(2)根据DB=CF,DB∥CF,可知四边形BDCF为平行四边形,再根据AC=BC,AD=DB,得出四边形BDCF是矩形.
试题解析:(1)证明:∵CF∥AB,
∴∠DAE=∠CFE,
在△ADE和△FCE中,
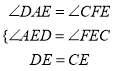
∴△ADE≌△FCE(AAS),
∴AD=CF,
∵AD=DB,
∴DB=CF;
(2)四边形BDCF是矩形,
证明:∵DB=CF,DB∥CF,
∴四边形BDCF为平行四边形,
∵AC=BC,AD=DB,
∴CD⊥AB,
∴平行四边形BDCF是矩形.


科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD:AE=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2 OG。其中正确结论的序号是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)3x+2(x2-y)-3(2x2+x-![]() y),其中x=
y),其中x=![]() ,y=-3;
,y=-3;
(2)3a2c-[2ab2-2(abc-![]() ab2)+3a2c]-abc,其中a=-
ab2)+3a2c]-abc,其中a=-![]() ,b=2,c=3.
,b=2,c=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )

A. 5 B. 8 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?若能,请给出求解过程.
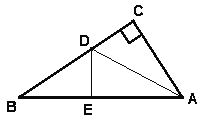
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com