
����Ŀ��ijѧУ������һ�������̳��˽��һ��A�����������B��������275Ԫ������A�����������B��������300Ԫ��
��1���ж�Ԫһ�η����������⣺��һ��A�������һ��B��������ۼ۸��Ƕ���Ԫ��
��2������ѧУ��ͬʱ�����������ͺŵ�����80��������A�����������С�ڵ���60��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
���𰸡���1��һ��A������50Ԫ��һ��B������75Ԫ����2����a��60ʱ��w����СֵΪ4500Ԫ��
��������
��1����һ��A������xԪ��һ��B������yԪ��������һ��A�����������B��������275Ԫ������A�����������B��������300Ԫ���з�������⼴�ɣ�
��2����A������a�����ܷ���wԪ���ɵ�w��6000��25a����һ�κ��������ʿ���⣮
�⣺��1����һ��A������xԪ��һ��B������yԪ��
��������ɵã�![]()
��ã�![]()
��һ��A������50Ԫ��һ��B������75Ԫ��
��2����A������a�����ܷ���wԪ��
��������ɵã�w��50a+75��80��a����6000��25a����a��60��
�ߩ�25��0��
��w����z�����������
�൱a��60ʱ��w����СֵΪ4500Ԫ��


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ�������ѳ�Ϊ������ϲ���Ľ�������֮һ��ͨ���ֻ����Լ������ߵIJ�������Ӧ���������ģ��Ա��ֻ����ݷ���С������12 000����С�첽��9 000�����ĵ�������ͬ����ÿ����1ǧ������С�����ߵIJ�����С���10������С��ÿ����1ǧ��������Ҫ���߶��ٲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ABD���ǵȱ������Σ���E��F�ֱ���BC��AC�ϣ�BE��CF��AE��BF���ڵ�G��

��1�����AGF�Ķ�����
��2������DG����AG��3��BG��2����DG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ��ӳ���ǣ�С���Ӽ����ܲ�ȥ�������������������һ������ߵ��ľߵ�ȥ��ʣ�Ȼ��ɢ���ؼң�����x��ʾʱ�䣬y��ʾС����ҵľ��룮
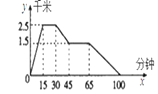
����ͼ��ش��������⣺
��1����������С���Ҷ�Զ��С���Ӽҵ����������˶���ʱ�䣿
��2�����������ľߵ��Զ��
��3��С�����ľߵ궺���˶���ʱ�䣿
��4��С�����ľߵ�ؼҵ�ƽ���ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������ABCD����������A��2����1����C��6��2������MΪy����һ�㣬��MAB�����Ϊ6�������������⣺
��1������B�������� ����
��2������BD����BD�ij���
��3����ֱ��д����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ຣ���������У�������У����٣�ij��˾��Ϊ�����ڽ�һ��ϣ��ѧУ���ס��������̶��ύ��Ͷ�귽������������ɸ���Ŀ������̶����õ�ʱ�����ҹ��̶ӵ�1.5�������ס������Ӻ�����ɸ���Ŀ������72�죮�ס������ӵ�����ɽ�У���̸�������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱߡ�ABC����
��1����ͼ1��P��Q��BC���ϵ����㣬AP=AQ����BAP=20�㣬���AQB�Ķ�����
��2����P��Q��BC���ϵ��������㣨�����B��C�غϣ�����P�ڵ�Q����࣬��AP=AQ����Q����ֱ��AC�ĶԳƵ�ΪM������AM��PM��
�������⽫ͼ2��ȫ��
��С��ͨ���۲졢ʵ��������룺�ڵ�P��Q�˶��Ĺ����У�ʼ����PA=PM��С������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1��Ҫ֤��PA=PM��ֻ��֤��APM�ǵȱ������Σ�
�뷨2����BA��ȡһ��N��ʹ��BN=BP��Ҫ֤��PA=PM��ֻ��֤��ANP�ա�PCM��
�뷨3�����߶�BP�Ƶ�B˳ʱ����ת60�㣬�õ��߶�BK��Ҫ֤PA=PM��ֻ��֤PA=CK��PM=CK��
����ο�������뷨������С��֤��PA=PM��һ�ַ������ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ��OA=OC�����������ߵ�����д�����º���a��b��c������ĸ�ĵ�ʽ��ʽ����![]() =��1����ac+b+1=0����abc��0����a��b+c��0��������ȷ�ĸ����ǣ��� ��
=��1����ac+b+1=0����abc��0����a��b+c��0��������ȷ�ĸ����ǣ��� ��

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ABC�У���BAC=90����AB=AC����BAD=30����AD=AE������EDC�Ķ���Ϊ��������

A.10��B.15��C.20��D.30��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com