
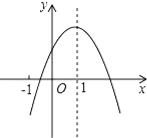
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
A. ①②③ B. ①③④ C. ③④⑤ D. ②③⑤
【答案】B
【解析】试题分析:①图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,-![]() =1,
=1,
∴b=-2a>0,
∴abc<0,
所以①正确;
②当x=-1时,由图象知y<0,
把x=-1代入解析式得:a-b+c<0,
∴b>a+c,
∴②错误;
③图象开口向下,与y轴交于正半轴,对称轴为x=1,
能得到:a<0,c>0,-![]() =1,
=1,
所以b=-2a,
所以4a+2b+c=4a-4a+c>0.
∴③正确;
④∵由①②知b=-2a且b>a+c,
∴2c<3b,④正确;
⑤图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,-![]() =1,
=1,
∴b=-2a,
∴a+b=a-2a=-a,m(ma+b)=m(m-2)a,
假设a+b<m(am+b),(m≠1的实数)
即-a<m(m-2)a,
所以(m-1)2<0,
不满足题意,所以假设不成立,
∴⑤不正确.
故正确结论是①、③,④.
故选:B.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示,则下列结论错误的是( )
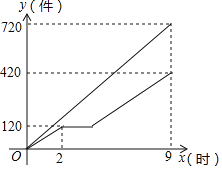
A.甲车间每小时加工服装80件
B.这批服装的总件数为1140件
C.乙车间每小时加工服装为60件
D.乙车间维修设备用了4小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=2,则下列结论正确的有( )个.
①ax2+bx+c=0(a≠0)有两个不相等的实数根
②3a﹣c>0
③a﹣b+c<0
④(0,y1)、(4,y2)在此二次函数的图象上,则y1<y2
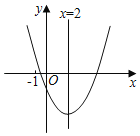
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届“一带一路”国际合作高峰论坛将于2019年4月在北京举行.为了让恩施特产走出大山,走向世界,恩施一民营企业计划生产甲、乙两种商品共10万件,销住“一带一路”沿线国家和地区.已知3件甲种商品与2件乙种商品的销售收入相同,1件甲种商品比2件乙种商品的销售收入少600元.甲、乙两种商品的销售利润分别为120元和200元
(1)甲、乙两种商品的销售单价各多少元?
(2)市场调研表明:所有商品能全部售出,企业要求生产乙种商品的数量不超过甲种商品数量的![]() ,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
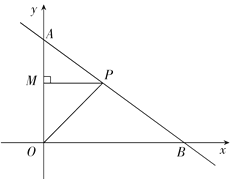
【题目】如图:一次函数![]() 的图象与坐标轴交于A、B两点,点P是函数
的图象与坐标轴交于A、B两点,点P是函数![]() (0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(1)当AP为何值时,△OPM的面积最大?并求出最大值;
(2)当△BOP为等腰三角形时,试确定点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两幅不完整的统计图.优秀人数条形统计图
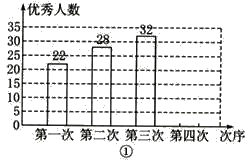
优秀率折线统计图
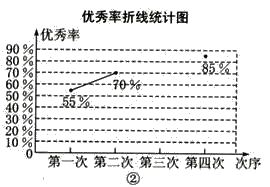
请根据以上两幅图,解答下列问题:
(1)该班总人数是________;
(2)根据计算,请你补全两幅统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系xOy中,抛物线![]() 的解析式为
的解析式为![]() ,将抛物线
,将抛物线![]() 平移后得到抛物线
平移后得到抛物线![]() ,若抛物线
,若抛物线![]() 经过点(0,2),且其顶点A的横坐标为最小正整数.
经过点(0,2),且其顶点A的横坐标为最小正整数.
(1)求抛物线![]() 的解析式;
的解析式;
(2)说明将抛物线![]() 如何平移得到抛物线
如何平移得到抛物线![]() ;
;
(3)若将抛物线![]() 沿其对称轴继续上下平移,得到抛物线
沿其对称轴继续上下平移,得到抛物线![]() ,设抛物线
,设抛物线![]() 的顶点为B,直线OB与抛物线
的顶点为B,直线OB与抛物线![]() 的另一个交点为C.当OB=OC时,求点C的坐标.
的另一个交点为C.当OB=OC时,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com