
【题目】如图,已知直线AB:y=![]() x+
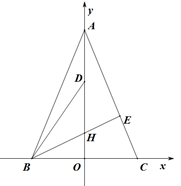
x+![]() 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
A. (0,4) B. (0,5) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
【答案】A
【解析】
作EF⊥BC于F,设AD=EC=x.利用勾股定理可得BD+BE=![]() +
+![]() =
=![]() +
+![]() ,要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到G(
,要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到G(![]() ,3),K(
,3),K(![]() ,
,![]() )的距离之和最小.
)的距离之和最小.
解:由题意A(0,![]() ),B(-3,0),C(3,0),
),B(-3,0),C(3,0),
∴AB=AC=8,
作EF⊥BC于F,设AD=EC=x.
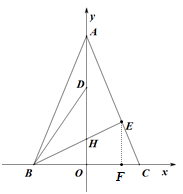
∵EF∥AO,
∴![]() ,
,
∴EF=![]() ,CF=
,CF=![]() ,
,
∵OH∥EF,
∴![]() ,
,
∴OH=![]() ,
,
∴BD+BE=![]() +
+![]() =
=![]() +
+![]() ,
,
要求BD+BE的最小值,相当于在x轴上找一点M(x,0),使得点M到K(![]() ,3),G(
,3),G(![]() ,
,![]() )的距离之和最小.
)的距离之和最小.

设G关于x轴的对称点G′(![]() ,
,![]() ),直线G′K的解析式为y=kx+b,
),直线G′K的解析式为y=kx+b,
则有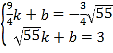 ,
,
解得k=![]() ,b=
,b=![]() ,
,
∴直线G′K的解析式为y=![]() x
x![]() ,
,
当y=0时,x=![]() ,
,
∴当x=![]() 时,MG+MK的值最小,此时OH=
时,MG+MK的值最小,此时OH=![]() =
=![]() =4,
=4,
∴当BD+BE的值最小时,则H点的坐标为(0,4),
故选:A.


科目:初中数学 来源: 题型:
【题目】计算
(1)4a2b(2b2-1)
(2)(x-2y)(y+2x)
(3)(6m2n-3m2)÷(-3m2)
(4)2019×2017-20182(用简便方法计算)
(5)先化简,再求值:![]() ;其中
;其中![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) | 1 | 2 | 3 | … | 50 |
p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+![]() .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加理化实验操作测试,学校进行了6次模测试,成绩如表所示:(单位:分)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 平均分 | 众数 | |
甲 | 7 | 9 | 9 | 9 | 10 | 10 | 9 | 9 |
乙 | 7 | 8 | 9 | 10 | 10 | 10 | a | b |
(1)根据图表信息,求表格中a,b的值;
(2)已知甲的成绩的方差等于1,请计算乙的成绩的方差;
(3)从平均数和方差相结合看,分析谁的成绩好些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:像(![]() +
+![]() )(
)(![]()
![]() )=3,
)=3,![]()
![]() =a(a≥0),(
=a(a≥0),(![]() +1)(
+1)(![]() ﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:
﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:![]() 与
与![]() ,
,![]() +1与
+1与![]() ﹣1,2
﹣1,2![]() +3
+3![]() 与2
与2![]() ﹣3
﹣3![]() 等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
例如:![]() ;
; ;
;
解答下列问题:
(1)3﹣![]() 与 互为有理化因式,将
与 互为有理化因式,将![]() 分母有理化得 .
分母有理化得 .
(2)计算:2﹣![]() ;
;
(3)观察下面的变形规律并解决问题.
①![]() =
=![]() ﹣1,
﹣1,![]() =
=![]()
![]() ,
,![]() =
=![]() ,…,若n为正整数,请你猜想:
,…,若n为正整数,请你猜想:![]() = .
= .
②计算:(![]() +
+![]() +
+![]() +…+
+…+![]() )×(
)×(![]() +1).
+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
在⊙I中,弦AF与DE相交于点Q,则AQQF=DQQE.你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,等边△ABC的边BC在x轴上,高AO在y轴的正半轴上,点Q(0,1)是等边△ABC的重心,过点Q的直线分别交边AB、AC于点D、E,直线DE绕点Q转动,设∠OQD=α(60°<α<120°),△ADE的外接圆⊙I交y轴正半轴于点F,连接EF.
(1)填空:AB= ;
(2)在直线DE绕点Q转动的过程中,猜想:![]() 与
与![]() 的值是否相等?试说明理由.
的值是否相等?试说明理由.
(3)①求证:AQ2=ADAE﹣DQQE;
②记AD=a,AE=b,DQ=m,QE=m(a、b、m、n均为正数),请直接写出mn的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com