
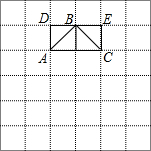
 阅读并解决问题
阅读并解决问题分析 方法迁移:根据题意画出图形,△ABC的面积等于正方形MNCP的面积减去三个小直角三角形的面积;
思维拓展:根据题意画出图形,△ABC的面积等于大矩形的面积减去三个小直角三角形的面积.
解答 解:方法迁移:
建立边长为1的正方形网格,在网格中画出△ABC,使△ABC三个顶点都在小正方形的顶点处,
AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,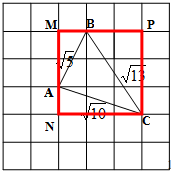 根据题意得:△ABC的面积等于正方形MNCP的面积减去三个小直角三角形的面积,即:
根据题意得:△ABC的面积等于正方形MNCP的面积减去三个小直角三角形的面积,即:
S△ABC=S正方形MNCP-S△AMB-S△CAN-S△CPB
=3×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×3=9-1-1.5-3=3.5.
思维拓展:
建立边长为m×n的矩形网格,在网格中画出△ABC,使△ABC三个顶点都在小正方形的顶点处,
其中AB=$\sqrt{(3m)^{2}+(2n)^{2}}$=$\sqrt{9{m}^{2}+4{n}^{2}}$,
AC=$\sqrt{(5m)^{2}+{n}^{2}}$=$\sqrt{25{m}^{2}+{n}^{2}}$,BC=$\sqrt{(2m)^{2}+{n}^{2}}$=$\sqrt{4{m}^{2}+{n}^{2}}$.如图所示:
则S△ABC=5m×2n-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×5m×n-$\frac{1}{2}$×2m×n=3.5mn.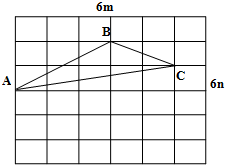
点评 本题考查了勾股定理、三角形面积的计算方法;熟练掌握勾股定理,在网格中画出△ABC是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
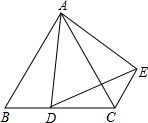 如图所示,△ABC是等边三角形,点D在BC上,△ABD经过逆时针方向旋转后到达△ACE的位置;
如图所示,△ABC是等边三角形,点D在BC上,△ABD经过逆时针方向旋转后到达△ACE的位置;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
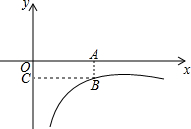 如图所示,点B是反比例函数y=$\frac{k}{x}$图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的函数关系式是y=-$\frac{4}{x}$.
如图所示,点B是反比例函数y=$\frac{k}{x}$图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的函数关系式是y=-$\frac{4}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 123.88×108 | B. | 1.2388×1010 | C. | 1.2×1010 | D. | 0.12388×1011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com