
分析 根据判别式的意义,由方程mx2-nx+2=0两根相等得到m≠0且n2-8m=0①,再设方程x2-4mx+3n=0的一个根是t,另一个根为3t,根据根与系数的关系得到t+3t=4m,t•3t=3n,消去t得m2=n②,解有①②组成的方程组得m=2,n=4,则方程x2-(k+m)x+(k-m)=0变形为x2-(k+2)x+(k-2)=0,然后计算该方程的判别式的值得到△=k2+12,则根据非负数的性质可得△>0,于是根据判别式得意义可判断方程x2-(k+m)x+(k-m)=0一定有实数根.
解答 证明:∵关于x的方程mx2-nx+2=0两根相等,
∴m≠0且n2-8m=0①,
∵方程x2-4mx+3n=0的一个根是另一个根的3倍,
设一个根为t,则另一个根为3t,
∴t+3t=4m,t•3t=3n,
∴m2=n②,
由①②得m=2,n=4,
∴方程x2-(k+m)x+(k-m)=0变形为x2-(k+2)x+(k-2)=0,
△=(k+2)2-4(k-2)
=k2+12,
∵k2≥0,
∴△>0,
∴方程x2-(k+m)x+(k-m)=0一定有实数根.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了根与系数的关系.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 方程x2=x的解是x=1 | |
| B. | 3的平方根是$\sqrt{3}$ | |
| C. | 有两边和一个角分别对应相等的两个三角形全等 | |
| D. | 连接任意四边形各边中点的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2-5x+4=0 | 1 | 4 | 5 | 4 |
| x2+7x+12=0 | -3 | -4 | -7 | 12 |
| x2-4x-5=0 | 5 | -1 | 4 | -5 |
| x2+bx+c=0 | $\frac{-b+\sqrt{{b}^{2}-4c}}{2}$ | $\frac{-b-\sqrt{{b}^{2}-4c}}{2}$ | -b | c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 较大的数减去一个较小的数差是正数 | |
| B. | 两个数的和大于任何一个加数 | |
| C. | 较小的数减去一个较大的数差是负数 | |
| D. | 任何一个数减去负数都要变大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列给出的四个命题:
①若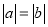 ,则
,则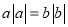 ;②若a2﹣5a+5=0,则
;②若a2﹣5a+5=0,则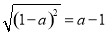 ;③
;③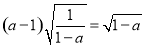
④若方程x2+px+q=0的两个实根中有且只有一个根为0,那么p≠0,q=0.
其中是真命题是( )
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
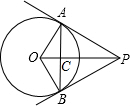 如图,点P为⊙O外一点,PA、PB分别与⊙O的相切于点A、B,线段AB、OP相交于点C,连接OA、OB,请写出两个你认为正确的结论(OA=OB除外):AP=BP,△AOP≌△BOP.
如图,点P为⊙O外一点,PA、PB分别与⊙O的相切于点A、B,线段AB、OP相交于点C,连接OA、OB,请写出两个你认为正确的结论(OA=OB除外):AP=BP,△AOP≌△BOP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
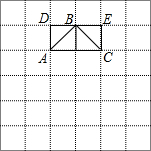 阅读并解决问题
阅读并解决问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com