
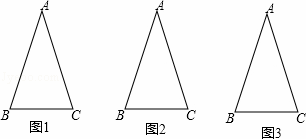
如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)
(1)在图1中画1条线段,使图中有2个等腰三角形,并直 接写出这2个等腰三角形的顶角度数分别是 108 度和 36 度;
接写出这2个等腰三角形的顶角度数分别是 108 度和 36 度;
(2)在图2中画2条 线段,使图中有4个等腰三角形;
线段,使图中有4个等腰三角形;
(3)继续按以上操作发现:在△ABC中画n条线段,则图中有 2n 个等腰三角形,其中有 n 个黄金等腰三角形.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于 CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是( )

A. SAS B.ASA C.AAS D. SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于 点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC.
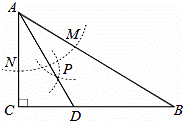
A. 1 B.2 C.3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A是直线l外一点,在l上取点B、C.按下列步骤作图:分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D.则四点A、B、C、D可组成的图形是 .
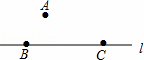
查看答案和解析>>
科目:初中数学 来源: 题型:
(如图,在△ABC中,BC=AC,且CD∥ AB,设△ABC的外心为O.
AB,设△ABC的外心为O.
(1)用尺规作出△ABC的外接圆O.(不写作法,保留痕迹)
(2)在(1)中,连接OC,并证明OC是AB的中垂线;
(3)直线CD与⊙O有何位置关系,试证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知下列命题:
①若a>b,则ac>bc;
②若a=1,则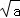 =a;
=a;
③内错角相等;
④90°的圆周角所对的弦是直径.
其中原命题与逆命题均为真命题的个数是( )
A. 1个 B.2个 C.3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
下列四个命题中,真命题是( )
A. 对角线互相垂直平分的四边形是正方形
B. 对角线垂直相等的四边形是菱形
C. 对角线相等且互相平分的四边形是矩形
D. 四边都相等的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com