
分析 (1)直接利用有理数的加减,再利用正负数的意义得出结论即可;
(2)利用有理数的加减求出各记录点离出发点的距离即可;
(3)求出所走的总路程即可.
解答 解:(1)(-605)+650+580+600+(-550)=675(米),
故B地在A地的东面,距A地675米;
(2)∵路程记录中各点离出发点的距离分别为:
605(米),
-605+650=45(米),
45+580=625(米),
625+600=1225(米),
1225-550=675(米),
∴最远处离A处1225米;
(3)|-605|+|650|+|580|+|600|+|-550|=2985(米),
故该同学在15分钟内一共跑了2985米.
点评 此题主要考查了正负数的定义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
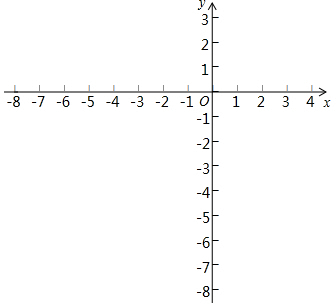 已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
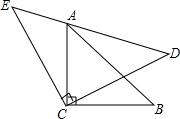 如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)
如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com