
分析 根据题意可得相遇时,甲走了6千米,乙走了5千米,相遇后,甲又走5km,乙走了6千米,设甲的速度为xkm/h,则乙的速度为$\frac{5}{\frac{6}{x}}$=$\frac{5}{6}$xkm/h,根据题意可得等量关系:甲走5千米的时间-乙走6千米的时间=22分钟,根据等量关系列出方程,再解即可.
解答 解:设甲的速度为xkm/h,则乙的速度为$\frac{5}{\frac{6}{x}}$=$\frac{5}{6}$xkm/h,由题意得:
$\frac{6}{\frac{5x}{6}}$-$\frac{5}{x}$=$\frac{22}{60}$,
解得:x=6,
经检验:x=6是原分式方程的解,
则乙的速度为$\frac{5}{6}$×6=5(km/h),
答:甲的速度为6km/h,则乙的速度为5km/h.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,设出未知数,表示出甲和乙的速度,再找出题目中的等量关系,列出方程,注意分式方程必须检验.


科目:初中数学 来源: 题型:选择题
| A. | 它的图象关于y轴对称 | |
| B. | 该抛物线开口向下 | |
| C. | 原点是该抛物线上的最高点 | |
| D. | 当x为任意实数时,函数值y总是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
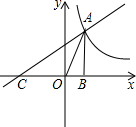 如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求:
如图,在平面直角坐标系中,直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A,与x轴交于点C,AB⊥x轴,垂足为B,此时点B(1,0).求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
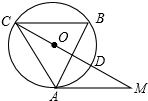 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com