
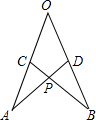
 如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )
如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ② | D. | ① |
分析 ①根据题中条件,由两边夹一角可得△AOD≌△BOC;
②根据全等三角形的性质得出对应角相等,又由已知得出AC=BD,可得△APC≌△BPD;
③根据等边三角形的性质和等量代换即可得到PC=PD.
解答 解:①在△AOD与△BOC中,
$\left\{\begin{array}{l}{OA=OB}\\{∠O=∠O}\\{OD=OC}\end{array}\right.$,
∴△AOD≌△BOC,故①正确;
②∵△AOD≌△BOC,
∴∠A=∠B,
又∵∠APC=∠BPD,
∴∠ACP=∠BDP,
OA-OC=OB-OD,即AC=BD,
在△APC与△BPD中,
$\left\{\begin{array}{l}{∠APC=∠BPD}\\{∠A=∠B}\\{AC=BD}\end{array}\right.$,
∴△APC≌△BPD,故②正确;
③∵△AOD≌△BOC,
∴AD=BC,
∵△APC≌△BPD,
∴AP=BP,
∴AD-AP=BC-BP,
∴PC=PD,故③正确.
故选:A.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA和HL,做题时,要根据已知条件结合图形进行思考.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
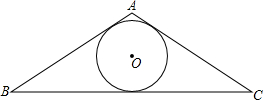 已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )| A. | 点O在△ABC的三边垂直平分线上 | |
| B. | 点O在△ABC的三个内角平分线上 | |
| C. | 如果△ABC的面积为S,三边长为a,b,c,⊙O的半径为r,那么r=$\frac{2S}{a+b+c}$ | |
| D. | 如果△ABC的三边长分别为5,7,8,那么以A、B、C为端点三条切线长分别为5,3,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 楼盘 | A | B | C | D |
| 销售面积(m2) | 10000 | 15000 | 10000 | 5000 |
| 销售单价(万元/m2) | 0.6 | 0.8 | 1 | 1.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com