
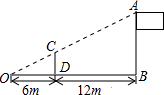
 (1)如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为9m.
(1)如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为9m.分析 (1)直接利用相似三角形的判定与性质得出$\frac{DC}{AB}$=$\frac{OD}{OB}$,即可得出答案;
(2)直接利用锐角三角函数关系得出答案.
解答 解:(1)由题意可得:DC∥AB,
则△CDO∽△ABO,
故$\frac{DC}{AB}$=$\frac{OD}{OB}$,
即$\frac{3}{AB}$=$\frac{6}{18}$,
解得:AB=9,
故答案为:9;
(2)由(1)得:tan∠AOB=$\frac{9}{18}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题主要考查了相似三角形的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
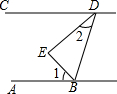 如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com