
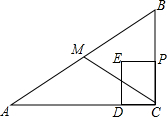
 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).分析 (1)根据DP∥AC得到成比例线段,代入计算即可;
(2)分点E在△ABC的内部、点E在△ABC的外部与AB相切和圆与CM相切三种情况进行分析,运用三角形的面积和锐角三角函数的概念进行解答即可.
解答 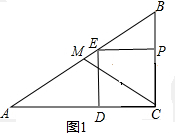 解:(1)如图1,∵四边形PCDE是正方形,
解:(1)如图1,∵四边形PCDE是正方形,
∴DP∥AC,
∴$\frac{EP}{AC}$=$\frac{BP}{BC}$,
即$\frac{t}{8}$=$\frac{6-t}{6}$,
解得t=$\frac{24}{7}$;
(2)如图2,当点E在△ABC的内部时,圆E与直线AB相切,EF⊥AB,且EF=1时,
连接AE、BE、CE,
∵∠ACB=90°,AC=8,BC=6,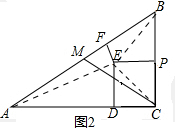
∴AB=10,
$\frac{1}{2}$×AB×EF+$\frac{1}{2}×AC×DE$+$\frac{1}{2}$×BC×EP=$\frac{1}{2}$×AC×BC,
$\frac{1}{2}$×10×1+$\frac{1}{2}$×8×t+$\frac{1}{2}$×6×t=$\frac{1}{2}$×8×6,
解得t=$\frac{19}{7}$;
如图3,当点E在△ABC的外部时,圆E与直线AB相切,EG⊥AB,且EG=1时,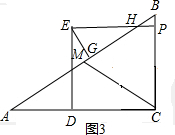
∵∠EGH=∠BPH,∠EHG=∠BHP,
∴∠GEH=∠PBH,
∴cos∠GEH=cos∠ABC=$\frac{BC}{AB}$=$\frac{3}{5}$,又EG=1,
∴EH=$\frac{5}{3}$,
∵$\frac{HP}{AC}$=$\frac{BP}{BC}$,∴HP=$\frac{24-4t}{3}$,
则$\frac{5}{3}$+$\frac{24-4t}{3}$=t,
解得t=$\frac{29}{7}$;
如图4,当圆E与直线CM相切时,EN=1,
作MR∥BC,则MR=$\frac{1}{2}$BC=3,CR=$\frac{1}{2}$AC=4,
∵点M是边AB的中点,
∴CM=$\frac{1}{2}$AB=5,
tan∠ACM=$\frac{MR}{RC}$=$\frac{3}{4}$,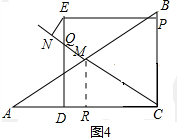
∴$\frac{QD}{CD}$=$\frac{3}{4}$,CD=t,
则QD=$\frac{3}{4}$t,EQ=$\frac{1}{4}$t,
∵∠NEQ=∠ACM,
∴$\frac{EN}{EQ}$=$\frac{1}{\frac{1}{4}t}$=$\frac{4}{5}$,
解得t=5.
点评 本题考查的是直线与圆相切、锐角三角函数和相似三角形的判定和性质,正确作出辅助线、灵活运用切线的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
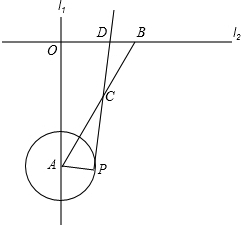 如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
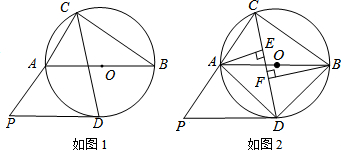
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
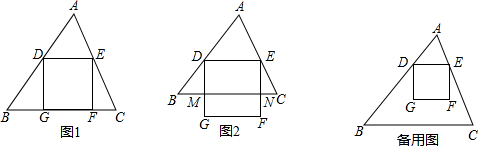
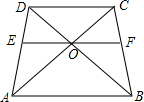 在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com