
【题目】如图:已知:点A(﹣4,0),B (0,3)分别是x、y轴上的两点.
(1)用尺规作图作出△ABO的外接圆⊙P;(不写作法,保留作图痕迹)
(2)求出⊙P向上平移几个单位后与x轴相切.
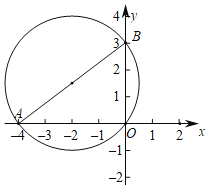
科目:初中数学 来源: 题型:
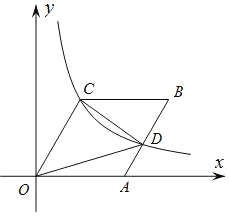
【题目】如图,在直角坐标系中,四边形OABC为菱形,OA在x轴的正半轴上,∠AOC=60°,过点C的反比例函数![]() 的图象与AB交于点D,则△COD的面积为_____.
的图象与AB交于点D,则△COD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
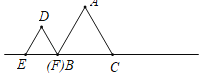
【题目】如图所示,已知△ABC与△DEF均为等边三角形,且AB=2,DB=1,现△ABC静止不动,△DEF沿着直线EC以每秒1个单位的速度向右移动设△DEF移动的时间为x,△DEF与△ABC重合的面积为y,则能大致反映y与x函数关系的图象是( )
A.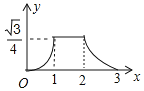 B.
B.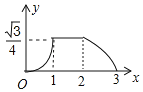
C. D.
D.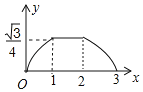
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,![]() ,
,![]() ,
,![]() 为格点,
为格点,![]() 为小正方形边的中点.
为小正方形边的中点.
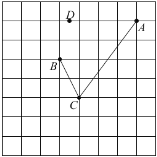
(1)![]() 的长等于_________;
的长等于_________;
(2)点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段
取得最小值时,请在如图所示的网格中,用无刻度的直尺,画出线段![]() ,
,![]() ,并简要说明点
,并简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明).
的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有![]() 个选项,第二道题有
个选项,第二道题有![]() 个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.
(1)如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;
(2)从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
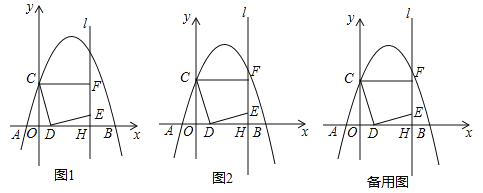
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
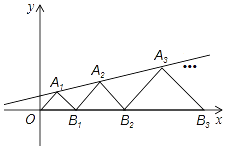
【题目】如图,在平面直角坐标系中,点A1,A2,A3…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
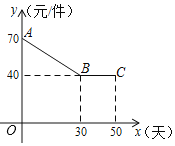
【题目】某工厂用![]() 天时间生产一款新型节能产品,每天生产的该产品被某网店以每件
天时间生产一款新型节能产品,每天生产的该产品被某网店以每件![]() 元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第
元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第![]() 天的生产成本
天的生产成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,第
(天)之间的关系如图所示,第![]() 天该产品的生产量
天该产品的生产量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]()
![]() 第
第![]() 天,该厂生产该产品的利润是 元;
天,该厂生产该产品的利润是 元;
![]() 设第
设第![]() 天该厂生产该产品的利润为
天该厂生产该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于![]() 元的共有多少天?
元的共有多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com