练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知△ABC的三个顶点的坐标分别是A（﹣2，3），点B（0，1），点C（2，2）．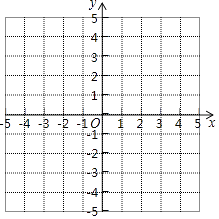

    （1）在所给的平面直角坐标系中画出△ABC．
    （2）直接写出点A到x轴，y轴的距离分别是多少？
    （3）求出△ABC的面积．

    【答案】
    （1）解：如图，△ABC为所作；


    （2）解：由图可知，点A（﹣2，3）到x轴的距离为3，到y轴的距离为2．
    （3）解：△ABC的面积=4×2﹣ ×2×2﹣ ×2×1﹣ ×4×1=3．
    【解析】（1）根据点A、B、C的坐标描点，连接三点从而可得到△ABC；
    （2）根据A到x轴的距离等于点A的纵坐标的绝对值，点A到y轴等于点A横坐标的绝对值求解即可；
    （3）将三角形的面积转化为一个矩形的面积与三个三角形的面积之差求解即可.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若a=2，b=﹣1，则a+2b+3的值为（ ）
    A.﹣1
    B.3
    C.6
    D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

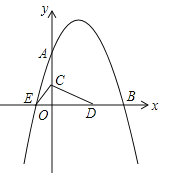
    【题目】如图，已知抛物线与坐标轴分别交于点A（0，8）、B（8，0）和点E，动点C从原点O开始沿OA方向以每秒1个单位长度移动，动点D从点B开始沿BO方向以每秒1个单位长度移动，动点C、D同时出发，当动点D到达原点O时，点C、D停止运动．

    （1）直接写出抛物线的解析式： ；

    （2）求△CED的面积S与D点运动时间t的函数解析式；当t为何值时，△CED的面积最大？最大面积是多少？

    （3）当△CED的面积最大时，在抛物线上是否存在点P（点E除外），使△PCD的面积等于△CED的最大面积？若存在，求出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某陶瓷商，为了促销决定卖一只茶壶，赠一只茶杯。某人共付款162元，买得茶壶茶杯共36只，已知每只茶壶15元，每只茶杯3元，问其中茶壶、茶杯各多少只？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）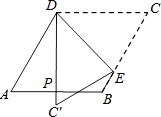
    A.78°
    B.75°
    C.60°
    D.45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】方程2x=10的解是___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据：5，7，10，5，7，5，6，这组数据的众数和中位数分别是（ ）

    A.10和7B.5和7C.5和6D.6和7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD． 求证：CE=BD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将边长为2的小正方形和边长为x的大正方形放在一起．

    （1）用x表示阴影部分的面积；
    （2）计算当x=5时，阴影部分的面积．

    查看答案和解析>>

    同步练习册答案