
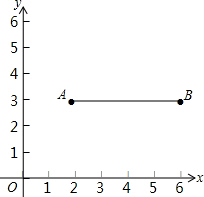
 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��3����B��6��3��������AB��������ƽ����һ��P���߶�AB�϶����ڵ�Q��ʹ��PQ��1����Ƶ�P���߶�AB�ġ��ڽ��㡱��
��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��3����B��6��3��������AB��������ƽ����һ��P���߶�AB�϶����ڵ�Q��ʹ��PQ��1����Ƶ�P���߶�AB�ġ��ڽ��㡱������ ��1������A��B������ó�AB��x�ᣬ���ݵ�P��ֱ��AB�ľ����1�������������2��x��6������2��y��4��Χ��ʱ�������߶�AB�ġ��ٽ��㡱��������������Ƿ���y�ķ�Χ�ڼ����Լ���A�����ߵ�A��ľ����1������B����ұߵ�B��ľ����1�������߶�AB�ġ��ٽ��㡱��
��2�������ֱ��y=x-1���߶�AB���ڣ�4��3����Ȼ�������������ۣ��ٵ�m��4ʱ�������߶�AB�ġ��ٽ��㡱��������ķ�Χ��2��n��4����n=2��n=4�ֱ����n=m-1�������Ӧ��mֵ�����ɵó���ĺ�����m�ķ�Χ��
��3����ͼ���ֱ����N1��N2�����꣬Ȼ����ݴ���ϵ�����ֱ���ú�����Ϊ2��������Ϊ3+$\sqrt{2}$�������Ϊ6��������Ϊ3-$\sqrt{2}$ʱ��ֱ��y=x+b��bֵ�����˿���b��ȡֵ��Χ��
���  �⣺��1����D���߶�AB�ġ��ڽ��㡱��
�⣺��1����D���߶�AB�ġ��ڽ��㡱��
��AD=$\sqrt{��2-\frac{7}{5}��^{2}+��3-\frac{19}{5}��^{2}}$=1��
��D��$\frac{7}{5}$��$\frac{19}{5}$�����߶�AB�ġ��ٽ��㡱��
�ʴ�Ϊ���ǣ�
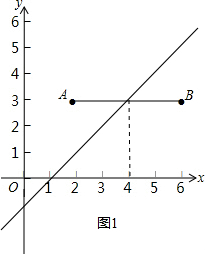
��2����ͼ1���ߵ�H��m��n�����߶�AB�ġ��ڽ��㡱����H��m��n����ֱ��y=x-1�ϣ�
��n=m-1��
ֱ��y=x-1���߶�AB���ڣ�4��3��
�ٵ�m��4ʱ����n=m-1��3��
��AB��x�ᣬ
���ʱ��H��m��n�����߶�AB�ľ�����n-3��
��0��n-3��1��
��4��m��5��
�ڵ�m��4ʱ����n=m-1��
��n��3��
��AB��x�ᣬ
���ʱ��H��m��n�����߶�AB�ľ�����3-n��
��0��3-n��1��
��3��m��4��
����������3��m��5��
��3������ͼ2��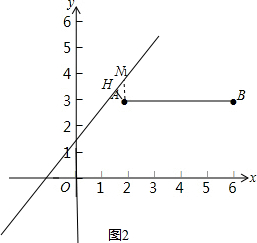
��ֱ��y=x+b��֪��AN1H=45�㣬
��PH=1��
��AN1=$\sqrt{2}$��
��N1��2��3+$\sqrt{2}$����
�Ѻ�����2��������3+$\sqrt{2}$����ֱ��y=x+b���ɵ�3+$\sqrt{2}$=2+b�����b=$\sqrt{2}$+1��
����ͼ3��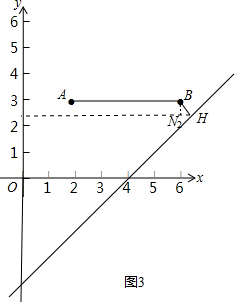
ͬ��֤��N2��6��3-$\sqrt{2}$����
�Ѻ�����6��������3-$\sqrt{2}$����ֱ��y=x+b���ɵ�3-$\sqrt{2}$=6+b�����b=-$\sqrt{2}$-3��
��b��ȡֵ��ΧΪ-$\sqrt{2}$-3��b��$\sqrt{2}$+1��
���� ���⿼����һ�κ����ۺ��⣬�漰�����ľ��빫ʽ������ϵ������ֱ�߽���ʽ������ֱ�������ε����ʵȣ�ͨ��������������ѧ���ķ�������ͽ��������������һ���dz��á��Ƚϵ��͵���Ŀ��


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
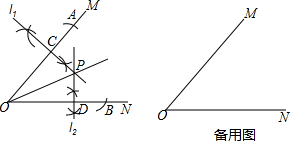
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
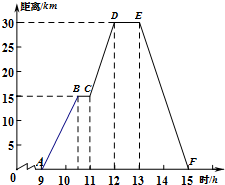 Сǿ�����г�ȥ���Σ�9ʱ������15ʱ���أ���ͼ��ʾ����ҵľ���y��ǧ�ף�����Ӧ��ʱ��x��ʱ��֮��ĺ�����ϵ��ͼ�������ͼ��Сǿ14ʱ��ҵľ����ǣ�������
Сǿ�����г�ȥ���Σ�9ʱ������15ʱ���أ���ͼ��ʾ����ҵľ���y��ǧ�ף�����Ӧ��ʱ��x��ʱ��֮��ĺ�����ϵ��ͼ�������ͼ��Сǿ14ʱ��ҵľ����ǣ�������| A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ƽ��ֱ������ϵxOy�У�������y=ax2+bx+1��a��0������A��-1��0����B��1��1������y�ύ�ڵ�C��
��ƽ��ֱ������ϵxOy�У�������y=ax2+bx+1��a��0������A��-1��0����B��1��1������y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com