
分析 (1)根据垂线段最短,则要使⊙O上有且只有一个点到直线l的距离等于2,则该点是点O到直线l的垂线段与圆的那个交点,此时圆的半径6-2=4;
(2)根据点O到直线l的距离为6,要使⊙O上有且只有三个点到直线l的距离等于2,则需要在此直线的两侧分别有一条和该直线的距离是2的直线分别和圆相交、相切.此时圆的半径是6+2=8;
(3)结合上述两种特殊情况即可对此题进行分情况考虑:当0<r<4时,或当r=4时,或当4<r<8时,或当r=8时,或当r>8时.
解答 解:(1)r=6-2=4,
故答案为:4;
(2)4<r<8;
(3)当0<r<4时,⊙O上到直线l的距离等于2的点的个数为0,
当r=4时,⊙O上到直线l的距离等于2的点的个数为1,
当4<r<8时,⊙O上到直线l的距离等于2的点的个数为2,
当r=8时,⊙O上到直线l的距离等于2的点的个数为3,
当r>8时,⊙O上到直线l的距离等于2的点的个数为4.
点评 本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.


科目:初中数学 来源: 题型:解答题
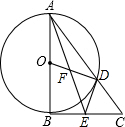 如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE,AE与OD交于点F.
如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE,AE与OD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如果$\frac{3x-2}{x+1}$=3+$\frac{m}{x+1}$,求m的值;
(1)如果$\frac{3x-2}{x+1}$=3+$\frac{m}{x+1}$,求m的值;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com