练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知,一次函数y=kx+b的图象与正比例函数y=x交于点A,并与y轴交于点B(0,4)，△AOB的面积为6，求kb的值．

    【答案】4或.

    【解析】

    一次函数经过点（0，4），代入即可求得b的值，即已知△AOB中，OB的值，根据△AOB的面积为6，即可求得k的值，从而求解．

    把(0,4)代入y=kx+b，得到b=4；

    则OB=4,设A的横坐标是m,则根据△AOB的面积为6,得到×4×|m|=6，解得m=±3.

    把x=±3代入正比例函数y=x,解得y=±1,则A的坐标是(3,1)或(3,1).

    当A是(3,1)时，代入y=kx+4，得到k=1.则kb=1×4=4；

    当A是(3,1)时,代入y=kx+4,得到k=,则kb=；

    故kb=4或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，三角形ABC三个顶点A，B，C的坐标分别为A（1，2），B（4，3），C（3，1）.把三角形A1B1C1向右平移4个单位长度，再向下平移3个单位长度，恰好得到三角形ABC，试写出三角形A1B1C1三个顶点的坐标，作出三角形ABC向右平移1个单位向下平移2个单位的图形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答下列应用题：

    ⑴某房间的面积为17.6m2，房间地面恰好由110块相同的正方形地砖铺成，每块地砖的边长是多少？

    ⑵已知第一个正方体水箱的棱长是60cm，第二个正方体水箱的体积比第一个水箱的体积的3倍还多81000 cm3，则第二个水箱需要铁皮多少平方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

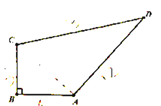
    【题目】如图，小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜，爸爸让小明计算这块土地的面积，以便估算产值，小明测得AB=4m,BC=3m,CD=13m.DA=12m.又已知∠B=90°，每平方米投入资金80元，预计销售后产值每平方米480元，试求出这块土地能产生多少利润?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（背景介绍）勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．

    （小试牛刀）把两个全等的直角三角形如图1放置，其三边长分别为a、b、c．显然，∠DAB=∠B=90°，AC⊥DE．请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理：

    S梯形ABCD= ，

    S△EBC= ，

    S四边形AECD= ，

    则它们满足的关系式为 ，经化简，可得到勾股定理．

    （知识运用）（1）如图2，铁路上A、B两点（看作直线上的两点）相距40千米，C、D为两个村庄（看作两个点），AD⊥AB，BC⊥AB，垂足分别为A、B，AD=25千米，BC=16千米，则两个村庄的距离为 千米（直接填空）；

    （2）在（1）的背景下，若AB=40千米，AD=24千米，BC=16千米，要在AB上建造一个供应站P，使得PC=PD，请用尺规作图在图2中作出P点的位置并求出AP的距离．

    （知识迁移）借助上面的思考过程与几何模型，求代数式最小值（0＜x＜16）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲从A出发向B行走，同时乙从B出发向A行走，如图相交于点P的两条线段里l1、l2分别表示甲、乙距离B的路程y（km）与已用时间x（h）之间的关系．
    （1）求甲乙行走的速度；
    （2）求l1、l2的表达式；
    （3）计算乙需多长时间到达A地．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．

    （1）求证：AB=CF；

    （2）连接DE，若AD=2AB，求证：DE⊥AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】填一填

    （1）已知，则________

    （2）一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=_________.

    （3）已知，则___________________；

    （4）已知，，则_________________；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等腰△ABC的外心，AD是圆O的切线，切点为A，过点C作CD≡∥AB，交AD于点D．连接AO并延长交BC于点M，连接AD，交过点C的直线于点P，且∠BCP=∠ACD．

    （1）判断直线PC与⊙O的位置关系，并说明理由；

    （2）若AB=12，BC=8．求PC的长．

    查看答案和解析>>

    同步练习册答案