Question

如图，Rt△ABC中，∠BAC=90°，AB=2，AC=4，D是BC边上一动点，G是BC边上的一动点，GE∥AD分别交AC、BA或其延长线于F、E两点

（1）如图1，当BC=5BD时，求证：EG⊥BC；

（2）如图2，当BD=CD时，FG+EG是否发生变化？证明你的结论；

（3）当BD=CD，FG=2EF时，DG的值=　　　　　　．

　

Answer 1

【考点】相似形综合题．

【分析】（1）利用勾股定理得出BC，进一步求得BD，根据“SAS”证得△BDA∽△BAC，得出∠BDA=∠BAC=90°，EG∥AD，进一步得出结论；

（2）当BD=CD时，FG+EG=2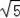不发生变化，利用△CFG∽△CAD，△ABD∽△AGE求得结论成立（也可作出辅助线，辅助线多种作法求得结论）；

（3）分两种情况：F在CA的延长线上和E在BA的延长线上，由此画出图形，利用相似得出结论．

【解答】证明：（1）如图1，

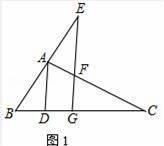
∵∠BAC=90°，AB=2，AC=4，

∴BC=2，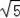

∵BC=5BD，

∴BD=，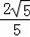

∴==

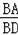
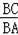
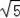
又∵∠DBA=∠ABC，

∴△BDA∽△BAC，

∴∠BDA=∠BAC=90°，

∵EG∥AD，

∴EG⊥BC．

（2）FG=EG=2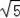不变，

证法1：如图2，

∵EG∥AD，

∴△CFG∽△CAD，

∴=，

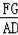
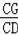
同理=，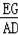

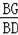
∵BD=CD，

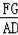
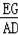
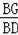
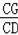
∴+=+=2，

∴EG+FG=2AD，

∵BD=CD，∠BAC=90°，

∴AD=BC=，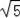

∴EG+FG=2AD=2．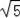

证法2：如图3，

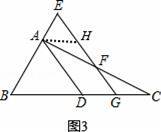
取EF的中点，易证四边形ADGH是平行四边形，

得出EG+FG=2GH=2AD=2．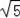

证法3：如图4，

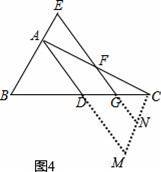
中线AD加倍到M，易证四边形AMNE是平行四边形，

得出EG+FG=EN=AM=2AD=2．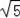

（3）如图5，

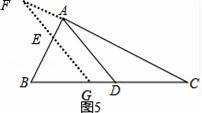
当BD=CD，FG=2EF时，

则GE=EF，

∵GE∥AD，AD∥GF，

∴△CFG∽△CAD，△ABD∽△BGE，

∴=， =，

∴==；

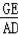
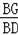
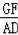
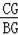
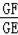
又BG+CG=2，

∴BG=，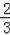

∴DG=BD=BG=；

如图6，

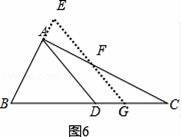
当BD=CD，FG=2EF时，

则GE=EF，

∵GE∥AD，AD∥GF，

∴△CFG∽△CAD，△ABD∽△AGE，

∴=， =，

∴==；

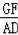
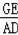
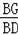
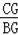
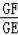
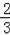
又BG+CG=2，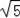

∴CG=，

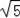
∴DG=CD﹣CG=．

综上所知DG为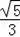或．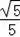

【点评】此题考查相似的综合，勾股定理的运用，相似三角形的判定与性质，关键在于结合题意，分类画出图形，探讨问题的答案．