
【题目】已知∠AOB=90°,OC是∠AOB的平分线,按以下要求解答问题.
(1)将三角板的直角顶点P在射线OC上移动,两直角边分别与OA,OB交于M,N,如图①,求证:PM=PN;
(2)将三角板的直角顶点P在射线OC上移动,一条直角边与OB交于N,另一条直角边与射线OA的反向延长线交于点M,并猜想此时①中的结论PM=PN是否成立,并说明理由 .
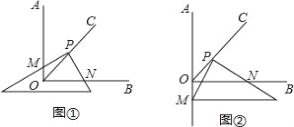
【答案】(1)见解析(2)成立
【解析】
(1)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证;
(2)过P作PE⊥OA,PF⊥OB,由OC为∠AOB的平分线,利用角平分线定理得到PE=PF,利用同角的余角相等得到一对角相等,利用ASA得到△PME与△PNF全等,利用全等三角形的对应边相等即可得证.
(1)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴![]()
∵![]()
∴∠MPE=∠NPF,
在△PME和△PNF中,
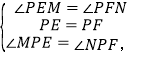
∴△PME≌△PNF(ASA),
∴PM=PN.
(2)过P作PE⊥OA于E,PF⊥OB于F,
∵OC是∠AOB的平分线,
∴![]()
∵![]()
∴∠MPE=∠NPF,
在△PME和△PNF中,
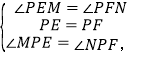
∴△PME≌△PNF(ASA),
∴PM=PN.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 81 | 74 | 85 |
丙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k< ![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求 ![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过 点A,C 画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )

A. SSS B. SAS C. ASA D. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q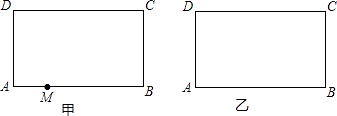
(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2 ,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.(1)△ABF与△DCE全等吗?请说明理由;(2)AB与CD平行吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国汉字听写大会”是由中央电视台和国家语言文学工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习,某校开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字,比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了如图两幅不完整的统计图.
根据以上信息回答下列问题:
(1)本次共随机抽取了名学生的听写结果,听写正确的汉字个数x在范围的人数最多;
(2)补全频数分布直方图;
(3)在扇形统计图中,请计算31≤x≤41所对应的扇形圆心角的大小;
(4)若该校共有1200名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在由6个边长为1的小正方形组成的方格中:
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com