
【题目】已知点![]() 是反比例函数
是反比例函数![]() 图象上的动点,
图象上的动点,![]() 轴,
轴,![]() 轴,分别交反比例函数
轴,分别交反比例函数![]() 的图象于点
的图象于点![]() 、
、![]() ,交坐标轴于
,交坐标轴于![]() 、
、![]() ,且
,且![]() ,连接
,连接![]() .现有以下四个结论:①
.现有以下四个结论:①![]() ;②在点
;②在点![]() 运动过程中,
运动过程中,![]() 的面积始终不变;③连接
的面积始终不变;③连接![]() ,则
,则![]() ;④不存在点
;④不存在点![]() ,使得
,使得![]() .其中正确的结论的序号是__________.
.其中正确的结论的序号是__________.
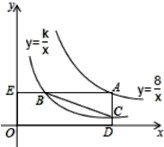
【答案】①②③
【解析】
①由反比例函数图象上点的坐标特征用函数a的代数式表示出来b,并找出点C坐标,根据AC=3CD,即可得出关于k的一元一次方程,解方程即可得出结论;
②根据①得出A、C的坐标,由AB∥x轴找出B点的坐标,由此即可得出AB、AC的长度,利用三角形的面积公式即可得出结论;
③已知B(![]() ,
,![]() ),C(a,
),C(a,![]() ),D(a,0),E(0,
),D(a,0),E(0,![]() )四点坐标,B、C、D、E四点坐标,经过B、C两点的直线斜率k1=
)四点坐标,B、C、D、E四点坐标,经过B、C两点的直线斜率k1=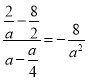 ,经过D、E两点的直线斜率k2=
,经过D、E两点的直线斜率k2=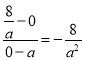 ,得出
,得出![]() ,即
,即![]()
④先假设![]() ,得到对应边成比例
,得到对应边成比例![]() ,列出关于a的等式,看a是否有解,即可求解.
,列出关于a的等式,看a是否有解,即可求解.
①∵A(a,b),且A在反比例函数![]() 的图象上,
的图象上,
∴![]()
∵AC∥y轴,且C在反比例函数![]() 的图象上,
的图象上,
∴C(a,![]() )
)
又∵AC=3CD,
∴AD=4CD,即![]()
∴k=2.
故①正确
②由①可知:A(a,![]() ),C(a,
),C(a,![]() )
)
∵AB∥x轴,
∴B点的纵坐标为![]() ,
,
∵点B在反比例函数![]() 的函数图象上,
的函数图象上,
∴![]() ,解得:x=
,解得:x=![]() ,
,
∴点B(![]() ,
,![]() ),
),
∴AB=a![]() =
=![]() ,AC=
,AC=![]()
![]() =
=![]()
∴S=![]() AB×AC=
AB×AC=![]() ×
×![]() ×
×![]() =
=![]()
∴在点A运动过程中,△ABC面积不变,始终等于![]()
故②正确
③连接DE,如图所示
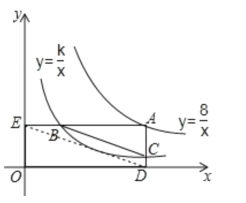
∵B(![]() ,
,![]() ),C(a,
),C(a,![]() )
)
∴经过B、C两点的直线斜率k1=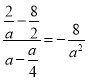
∵![]() 轴,
轴,![]() 轴
轴
∴D(a,0),E(0,![]() )
)
∴经过D、E两点的直线斜率k2=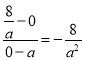
∴![]() ,即
,即![]()
故③正确
④假设![]()
∴![]()

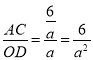
∴![]()
解得![]()
∴当![]() 时,
时,![]()
故④错误
故答案为:①②③


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
例:若代数式![]() ,求a的取值.
,求a的取值.
解:原式=![]() ,
,
当a<2时,原式=(2-a)+(4-a)=6-2a=2,解得a=2(舍去);
当2≤a<4时,原式=(a-2)+(4-a)=2=2,等式恒成立;
当a≥4时,原式=(a-2)+(a-4)=2a-6=2,解得a=4;
所以,a的取值范围是2≤a≤4.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)当3≤a≤7时,化简:![]() =_________;
=_________;
(2)请直接写出满足![]() =5的a的取值范围__________;
=5的a的取值范围__________;
(3)若![]() =6,求a的取值.
=6,求a的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=x2+2x+3的图象有以下说法:其中正确的个数是( )
①它开口向下;②它的对称轴是过点(﹣1,3)且平行于y轴的直线;③它与x轴没有公共点;④它与y轴的交点坐标为(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,
是菱形,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,设点
,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,则下列图象能正确反映
,则下列图象能正确反映![]() 与
与![]() 之间的函数关系的是( ).
之间的函数关系的是( ).
A.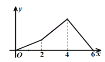 B.
B.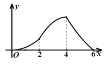 C.
C.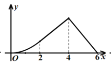 D.
D.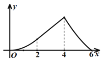
查看答案和解析>>
科目:初中数学 来源: 题型:
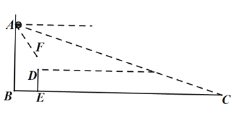
【题目】如图,在教室前面墙壁![]() 处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点
处安装了一个摄像头,当恰好观测到后面墙壁与底面交接处点![]() 时,摄像头俯角约为
时,摄像头俯角约为![]() ,受安装支架限制,摄像头观测的俯角最大约为
,受安装支架限制,摄像头观测的俯角最大约为![]() ,已知摄像头安装点高度
,已知摄像头安装点高度![]() 约为
约为![]() 米,摄像头与安装的墙壁之间距离忽略不计,
米,摄像头与安装的墙壁之间距离忽略不计,
![]() 求教室的长(教室前后墙壁之间的距离
求教室的长(教室前后墙壁之间的距离![]() 的值);
的值);
![]() 若第一排桌子前边缘与前面墙壁的距离
若第一排桌子前边缘与前面墙壁的距离![]() 为
为![]() 米, 桌子的高度
米, 桌子的高度![]() 为
为![]() 米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (
米,那么第一排桌子是否在监控范围内?如果不在,应该怎样移动? (![]() ,精确到
,精确到![]() 米)
米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 图象的顶点在一次函数
图象的顶点在一次函数![]() 的图象上,则称
的图象上,则称![]() 为
为![]() 的中雅函数,如:
的中雅函数,如:![]() 是
是![]() 的中雅函数.
的中雅函数.
(1)判断二次函数![]() 是否为一次函数
是否为一次函数![]() 的中雅函数,并说明理由;
的中雅函数,并说明理由;
(2)若关于![]() 的一次函数
的一次函数![]() 的中雅函数
的中雅函数![]() 与
与![]() 轴两个交点间的距离为
轴两个交点间的距离为![]() ,求直线
,求直线![]() 与坐标轴所围三角形的面积;
与坐标轴所围三角形的面积;
(3)已知关于![]() 的一次函数
的一次函数![]() 的中雅函数为
的中雅函数为![]() ,与
,与![]() 平行的直线
平行的直线![]() 交中雅函数
交中雅函数![]() 的图象于
的图象于![]() 、
、![]() 两点,若
两点,若![]() 轴上有且仅有一个点
轴上有且仅有一个点![]() ,使得
,使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
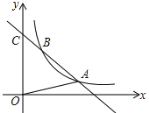
【题目】如图,一次函数的图象与y轴交于C(0,8),且与反比例函数y=![]() (x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点.
⑴求△AOC的面积;
⑵若![]() =4,求反比例函数和一次函数的解析式.
=4,求反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,BC=![]() AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
(1)判断四边形ABCE的形状,并说明理由;
(2)如果AB=4,∠D=30°,点P为BE上的动点,求△PAF的周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分别找一个点M、N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )

A.130°B.120°C.160°D.100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com