
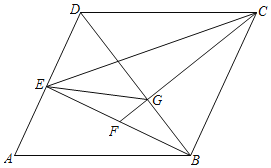
【题目】如图,在四边形ABCD中,BC∥AD,BC=![]() AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
(1)判断四边形ABCE的形状,并说明理由;
(2)如果AB=4,∠D=30°,点P为BE上的动点,求△PAF的周长的最小值.

【答案】(1)四边形ABCE是菱形,理由见解析;(2)△PAF的周长的最小值为![]() +2.
+2.
【解析】
(1)先证明四边形ABCE是平行四边形,再结合直角三角形斜边中线的性质得出CE=AE,从而可得到四边形ABCE是菱形;
(2)当PA+PF最小时,△PAF的周长最小.由(1)知四边形ABCE是菱形,得点A、C关于BE对称,得出PC=AP,即点P为CF与BE的交点时,C,P,F三点共线,PA+PF=PC+PF最小,此时△PAF的周长=PA+PF+AF=CF+AF.再证明△ACE是等边三角形,得AC=AE=CE=4,又根据AF=![]() AE=2,结合勾股定理可得出CF的长,从而可得出结果.
AE=2,结合勾股定理可得出CF的长,从而可得出结果.
解:(1)四边形ADCE是菱形,理由如下:
∵点E是AD的中点,∴AE=![]() AD.
AD.
∵BC=![]() AD,∴AE=BC.
AD,∴AE=BC.
∵BC∥AD,即BC∥AE.
∴四边形ABCE是平行四边形.
∵AC⊥CD,点E是AD的中点,
∴CE=AE,
∴四边形ABCE是菱形;
(2)由(1)得,四边形ABCE是菱形.
∴AE=EC=AB=4,且点A、C关于BE对称,∴AP=CP.
∴当PA+PF最小时,△PAF的周长最小,
即点P为CF与BE的交点时,C,P,F三点共线,PA+PF=PC+PF最小,
此时△PAF的周长=PA+PF+AF=CP+PE+AF=CF+AF.
在Rt△ACD中,点E是AD的中点,则CE=DE,
∴∠ECD=∠D=30°,∴∠ACE=90°-30°=60°,
∴△ACE是等边三角形,
∴AC=AE=CE=4.
∵AF=EF,∴CF⊥AE,
∵点F是AE的中点,AF=![]() AE=2.
AE=2.
∴CF=![]() ,
,
∴△PAF的周长最小值=CF+AF=![]() +2.
+2.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过B作BE⊥AD于点E,过点C作CF⊥BD分别与BD、BE交于点G、F,连接GE,已知AB=BD,CF=AB.
(1)若∠ABE=30°,AB=6,求△ABE的面积;
(2)求证:GE=![]() BG.
BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
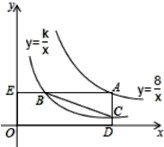
【题目】已知点![]() 是反比例函数
是反比例函数![]() 图象上的动点,
图象上的动点,![]() 轴,
轴,![]() 轴,分别交反比例函数
轴,分别交反比例函数![]() 的图象于点
的图象于点![]() 、
、![]() ,交坐标轴于
,交坐标轴于![]() 、
、![]() ,且
,且![]() ,连接
,连接![]() .现有以下四个结论:①
.现有以下四个结论:①![]() ;②在点
;②在点![]() 运动过程中,
运动过程中,![]() 的面积始终不变;③连接
的面积始终不变;③连接![]() ,则
,则![]() ;④不存在点
;④不存在点![]() ,使得
,使得![]() .其中正确的结论的序号是__________.
.其中正确的结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,将△ABC绕点B顺时针旋转60°,得到△BDE,连结DC交AB于点F,则△ACF与△BDF的周长之和为( )
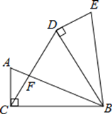
A.48B.50C.55D.60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半径为1的⊙O的直径,点C在⊙O上,∠CAB=30°,D为劣弧CB的中点,点P是直径AB上一个动点,则PC+PD的最小值为( )
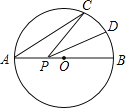
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx﹣2的图象与x轴交于点A(4,0),与y轴交于点B,且过点C (3,﹣2).

(1)求二次函数表达式;
(2)若点P为抛物线上第一象限内的点,且S△PBA=5,求点P的坐标;
(3)在AB下方的抛物线上是否存在点M,使∠ABO=∠ABM?若存在,求出点M到y轴的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
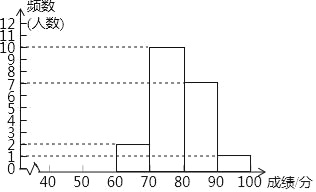
【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com