
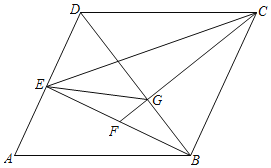
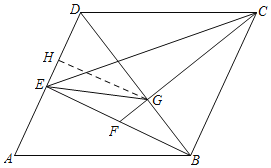
【题目】如图,在ABCD中,过B作BE⊥AD于点E,过点C作CF⊥BD分别与BD、BE交于点G、F,连接GE,已知AB=BD,CF=AB.
(1)若∠ABE=30°,AB=6,求△ABE的面积;
(2)求证:GE=![]() BG.
BG.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由含30°角直角三角形性质得出AE=![]() AB=3,由勾股定理得出BE=
AB=3,由勾股定理得出BE=![]() =3
=3![]() ,由三角形面积公式即可得出结果;
,由三角形面积公式即可得出结果;
(2)由平行四边形的性质得出AD=BC,AD∥BC,则∠ADB=∠CBD,证出∠BFC=∠BDE,得出∠CBG=∠BFG,由AAS证明△DEB≌△FBC得出BF=DE,BE=BC=2DE,设DE=x,则BE=BC=AD=2x,CF=BD=AB=![]() x,S△BCF=
x,S△BCF=![]() CFBG=
CFBG=![]() BFBC,求得BG=
BFBC,求得BG=![]() x,DG=
x,DG=![]() x,过G作GH⊥AD于H,由sin∠EDG=
x,过G作GH⊥AD于H,由sin∠EDG=![]() =
=![]() ,求得GH=
,求得GH=![]() x,由cos∠EDG=
x,由cos∠EDG=![]() =
=![]() ,求得DH=
,求得DH=![]() x,EH=DE﹣DH=
x,EH=DE﹣DH=![]() x,由勾股定理求出EG=
x,由勾股定理求出EG=![]() =
=![]() ,即可得出结论.
,即可得出结论.
(1)解:∵BE⊥AD,∠ABE=30°,
∴AE=![]() AB=3,BE=
AB=3,BE=![]() =
=![]() =3
=3![]() ,
,
∴S△ABE=![]() AEBE=
AEBE=![]() ×3×3
×3×3![]() =
=![]() ;
;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵∠FGB=∠BED=90°,∠FBG=∠DBE
∴∠BFC=∠BDE,
∴∠CBG=∠BFG,
∵∠CGB=∠BGF=90°,
∴∠BCF=∠DBE,
∴∠CBF=∠BCG+∠CBG=90°,
∵BE⊥AD,AB=BD,
∴AE=DE,
∵AB=BD,CF=AB,
∴CF=BD,
在△DEB和△FBC中, ,
,
∴△DEB≌△FBC(AAS),
∴BF=DE,BE=BC=2DE,
设DE=x,则BE=BC=AD=2x,CF=BD=AB=![]() x,
x,
S△BCF=![]() CFBG=
CFBG=![]() BFBC,
BFBC,
即:![]() xBG=x2x,
xBG=x2x,
∴BG=![]() x,
x,
∴DG=![]() x﹣
x﹣![]() x=
x=![]() x,
x,
过G作GH⊥AD于H,如图所示:
sin∠EDG=![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
∴GH=![]() x,
x,
cos∠EDG=![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
∴DH=![]() x,
x,
EH=DE﹣DH=x﹣![]() x=
x=![]() x,
x,
∴EG=![]() =
=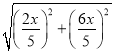 =
=![]() ,
,
∴![]() =
=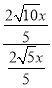 =
=![]() ,
,
∴EG=![]() BG.
BG.


科目:初中数学 来源: 题型:
【题目】目前,我国的空气质量得到了大幅度的提高.现随机调查了某城市1个月的空气质量情况,并将监测的结果绘制成如下的两幅不完整的统计图.
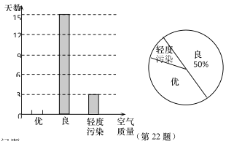
请根据图中提供的信息,解答下面的问题:
(1)本次调查中,一共调查的天数为_______天;扇形图中,表示“轻度污染”的扇形的圆心角为______度;
(2)将条形图补充完整;
(3)估计该城市一年(以365天计算)中,空气质量未达到优的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
例:若代数式![]() ,求a的取值.
,求a的取值.
解:原式=![]() ,
,
当a<2时,原式=(2-a)+(4-a)=6-2a=2,解得a=2(舍去);
当2≤a<4时,原式=(a-2)+(4-a)=2=2,等式恒成立;
当a≥4时,原式=(a-2)+(a-4)=2a-6=2,解得a=4;
所以,a的取值范围是2≤a≤4.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)当3≤a≤7时,化简:![]() =_________;
=_________;
(2)请直接写出满足![]() =5的a的取值范围__________;
=5的a的取值范围__________;
(3)若![]() =6,求a的取值.
=6,求a的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() 同时,点
同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 接,交
接,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() .解答下列问题:
.解答下列问题:
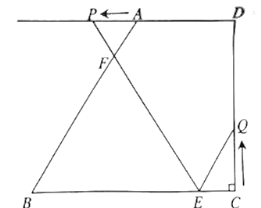
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() , 求
, 求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)连接![]() .是否存在某一时刻
.是否存在某一时刻![]() , 使点
, 使点![]() 在
在![]() 的垂直平分线上,若存在,求出的值;若不存在,说明理由.
的垂直平分线上,若存在,求出的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人驾车分别从A、B两地相向而行,乙出发半小时后甲出发,甲出发1.5小时后汽车出现故障,于是甲停下修车,半小时后甲修好后继续沿原路按原速与乙相遇,相遇后甲随即调头以原速返回A地,乙也继续向A地行驶,甲、乙两车之间的距离(y/千米)与甲驾车时间x(小时)之间的关系如图所示,当乙到达A地时,甲距离B地_____千米.
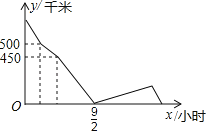
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=x2+2x+3的图象有以下说法:其中正确的个数是( )
①它开口向下;②它的对称轴是过点(﹣1,3)且平行于y轴的直线;③它与x轴没有公共点;④它与y轴的交点坐标为(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,
是菱形,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,设点
,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,则下列图象能正确反映
,则下列图象能正确反映![]() 与
与![]() 之间的函数关系的是( ).
之间的函数关系的是( ).
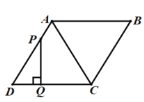
A.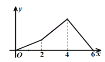 B.
B.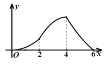 C.
C.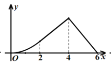 D.
D.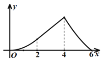
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,BC=![]() AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
AD,点E为AD的中点,点F为AE的中点,AC⊥CD,连接BE、CE、CF.
(1)判断四边形ABCE的形状,并说明理由;
(2)如果AB=4,∠D=30°,点P为BE上的动点,求△PAF的周长的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com