
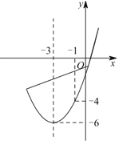
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 经过点
经过点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③若点
;③若点![]() 在抛物线上,则
在抛物线上,则![]() ;④关于
;④关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]() 和
和![]() ,其中正确的是_____.
,其中正确的是_____.
【答案】①②④
【解析】
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的顶点坐标可对②进行判断;由顶点坐标得到抛物线的对称轴为直线x=-3,则根据二次函数的性质可对③进行判断;根据抛物线的对称性得到抛物线y=ax2+bx+c上的点(-1,-4)的对称点为(-5,-4),则可对④进行判断.
∵抛物线与x轴有2个交点,
∴![]()
即![]() ,所以①正确;
,所以①正确;
∵抛物线的顶点坐标为(3,6),
即x=3时,函数有最小值,
∴![]() ,所以②正确;
,所以②正确;
∵抛物线的对称轴为直线x=3,
而点(2,m),(5,n)在抛物线上,
∴m<n,所以③错误;
∵抛物线![]() 经过点(1,4),
经过点(1,4),
而抛物线的对称轴为直线x=3,
∴点(1,4)关于直线x=3的对称点(5,4)在抛物线上,
∴关于x的一元二次方程![]() 的两根为5和1,所以④正确.
的两根为5和1,所以④正确.
故答案为:①②④


科目:初中数学 来源: 题型:
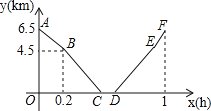
【题目】从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为 km/h,他在乙地休息了 h.
(2)分别求线段AB、EF所对应的函数关系式.
(3)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
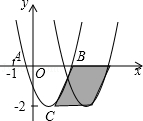
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0
②a﹣b+c<0
③阴影部分的面积为4
④若c=﹣1,则b2=4a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() ),销售量为
),销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①当
.该超市根据以往的销售经验得出以下的销售规律:①当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 与
与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 的关系式为 ;
的关系式为 ;
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若超市希望第![]() 天到第
天到第![]() 天的日销售利润
天的日销售利润![]() (元)随
(元)随![]() 的增大而增大,则需要在当天销售价格的基础上涨
的增大而增大,则需要在当天销售价格的基础上涨![]() 元/
元/![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阿里巴巴电商对贫困地区一种特色农产品进行网上销售,按原价每件300元出售,一个月可卖出100件,通过市场调查发现,售价每件降低10元,月销售件数增加20件
(1)已知该农产品的成本是每件200元,在保持月利润不变的情况下,尽快下手完毕,则售价应定为多少元?
(2)小红返校在附近线下超市也有该农产品销售,并且标价为每件300元,买五送一,在(1)的条件下,小红想要用最优惠的价格购买38件该农产品,应该选择在线上购买还是线下超市购买?
查看答案和解析>>
科目:初中数学 来源: 题型:
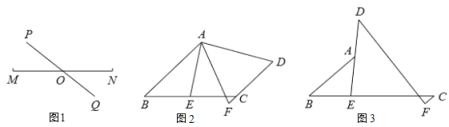
【题目】(1)操作:如图![]() ,点
,点![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() ,请利用图
,请利用图![]() 画出一对以点
画出一对以点![]() 为对称中心的全等三角形,(不写画法).
为对称中心的全等三角形,(不写画法).
根据上述操作得到的经验完成下列探究活动:
(2)探究一:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,试探究线段
,试探究线段![]() 与
与![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
(3)探究二,如图![]()
![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运如红脸代表忠心耿直,黑脸代表强悍勇猛现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.

(1)请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率(图案为“红脸”的两张卡片分别记为![]() 、
、![]() ,图案为“黑脸”的卡片记为
,图案为“黑脸”的卡片记为![]() );
);
(2)若第一次抽出后不放回,请直接写出求抽出的两张卡片上的图案都是“红脸”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价少20元,若购进甲商品5件和乙商品4件共需要1000元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件145元,乙种商品的售价为每件120元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于870元,则甲种商品至少可购进多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com