
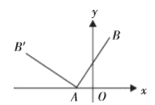
【题目】如图,在平面直角坐标系中,已知![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,则
,则![]() 的坐标为______________
的坐标为______________
 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
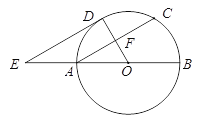
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=2时,求出四边形ACDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某渔业公司为了解投资收益情况,调查了旗下的养鱼场和远洋捕捞队近 10 个月的利润情况.根据收集的数据得知,近 10 个月总投资养鱼场 1 千万,获得的月利润频数分布表如下:
月平均利润(单位:千万元) | -0.2 | -0.1 | 0 | 0.1 | 0.3 |
频数 | 2 | 1 | 1 | 2 | 4 |
近 10 个月总投资远洋捕捞队 1 千万,获得的月利润频数分布表如下:
月平均利润(单位:千万元) | -0.3 | -0.1 | 0.1 | 0.3 | 0.5 |
频数 | 1 | 2 | 2 | 3 | 2 |
(1)根据上述数据,分别计算近 10 个月养鱼场和远洋捕捞队的月平均利润;
(2)公司计划用 6 千万的资金投资养鱼场和远洋捕捞队,受养鱼场和捕捞队规模大小的影响,要求投资养鱼场的资金不少于投资远洋捕捞队的资金的 2 倍.根据调查数据,给出公司分配投资资金额的建议,使得公司投资这两个项目的月平均利润之和最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
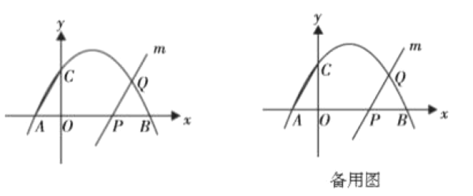
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是射线
是射线![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() ,与
,与![]() 轴右侧的抛物线交于点
轴右侧的抛物线交于点![]() .点
.点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒1个单位长度的速度向右运动,设点
以每秒1个单位长度的速度向右运动,设点![]() 运动的时间为t秒.请解答下列问题:
运动的时间为t秒.请解答下列问题:
(1)求直线AC的表达式与点![]() 的坐标;
的坐标;
(2)在点![]() 运动的过程中,若以点
运动的过程中,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求运动的时间
为顶点的四边形是平行四边形,求运动的时间![]() ;
;
(3)设点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,
①点![]() 的坐标为 (用含
的坐标为 (用含![]() 的代数式表示,结果需化简);
的代数式表示,结果需化简);
②当点![]() 落在抛物线
落在抛物线![]() 的对称轴上且点
的对称轴上且点![]() 在线段
在线段![]() 上时,在平面内是否存在点F,使得以点
上时,在平面内是否存在点F,使得以点![]() ,
,![]() ,
,![]() ,F为顶点的四边形为菱形?若存在,请求出此时点F的坐标;若不存在,请说明理由.
,F为顶点的四边形为菱形?若存在,请求出此时点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
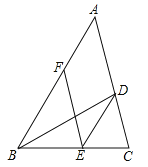
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=4,求平行四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com