
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОyЃНax2+bxЉ3Й§AЃЈ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉЁЂCШ§ЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуPЪЧBCЩЯЗНХзЮяЯпЩЯвЛЕуЃЌзїPQЁЮyжсНЛBCгкQЕуЃЎЧыЮЪЪЧЗёДцдкЕуPЪЙЕУЁїBPQЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгACЃЌЕуDЪЧЯпЖЮABЩЯвЛЕуЃЌзїDEЁЮBCНЛACгкEЕуЃЌСЌНгBEЃЎШєЁїBDEЁзЁїCEBЃЌЧѓDЕузјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+4xЉ3ЃЛЃЈ2ЃЉДцдкЕуPЪЙЕУЁїBPQЮЊЕШбќШ§НЧаЮЃЌPЕузјБъЮЊP1ЃЈ1ЃЌ0ЃЉЃЌP2ЃЈ2ЃЌ1ЃЉЃЌ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтПЩЕУХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЯШЧѓГіжБЯп![]() ЕФНтЮіЪНЃЌЗжШ§жжЧщПіЃКЕБ
ЕФНтЮіЪНЃЌЗжШ§жжЧщПіЃКЕБ![]() ЪБЃЌЩш
ЪБЃЌЩш![]() ЃЌПЩБэЪОГіШ§ЬѕЯпЖЮГЄЃЌдђНтЗНГЬПЩЧѓГіPЕузјБъЃЛ
ЃЌПЩБэЪОГіШ§ЬѕЯпЖЮГЄЃЌдђНтЗНГЬПЩЧѓГіPЕузјБъЃЛ
ЃЈ3ЃЉжЄЕУ![]() ПЩЕУБШР§ЯпЖЮЧѓГіAEГЄЃЌЕБ
ПЩЕУБШР§ЯпЖЮЧѓГіAEГЄЃЌЕБ![]() ЪБПЩЧѓГіDЕузјБъЃЎ
ЪБПЩЧѓГіDЕузјБъЃЎ
ЃЈ1ЃЉНЋ![]() ДњШы
ДњШы![]() ЕУЃК
ЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ХзЮяЯпНтЮіЪН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉДцдкЕуPЪЙЕУЁїBPQЮЊЕШбќШ§НЧаЮЃЌ
ЁпBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌ
ЁрЩшжБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩЗжШ§жжЧщПіПМТЧЃК
ЃЌПЩЗжШ§жжЧщПіПМТЧЃК
ЂйЕБ![]() ЪБЃЌгЩЬтвтЕУPЁЂQЙигкxжсЖдГЦЃЌ
ЪБЃЌгЩЬтвтЕУPЁЂQЙигкxжсЖдГЦЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂлЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌ
ЃЌ
ећРэЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
злКЯвдЩЯПЩЕУPЕузјБъЮЊP1ЃЈ1ЃЌ0ЃЉЃЌP2ЃЈ2ЃЌ1ЃЉЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпЁїBDEЁзЁїCEBЃЌ
ЁрЁЯABEЃНЁЯACBЃЌ
ЁпЁЯBAEЃНЁЯCABЃЌ
ЁрЁїABEЁзЁїACBЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]()
Ёр![]()
Ёп![]() ЃЌ
ЃЌ
Ёр![]()
Ёр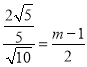
Ёр![]()
Ёр![]() .
.


 УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃдЫЖЏЛсЕФСЂЖЈЬјдЖКЭ1ЗжжгЬјЩўСНИіЕЅЯюБШШќЗжГЩдЄШќКЭОіШќСНИіНзЖЮЃЎЯТБэЮЊВЮМгетСНЯюБШШќЕФ10УћбЇЩњЕФдЄШќГЩМЈЃК
бЇЩњБрКХ ГЩМЈ ЯюФП | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
СЂЖЈЬјдЖЃЈЕЅЮЛЃКУзЃЉ | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1ЗжжгЬјЩўЃЈЕЅЮЛЃКДЮЃЉ | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
дкет10УћбЇЩњжаЃЌЭЌЪБНјШыСНЯюОіШќЕФжЛга6ШЫЃЌНјШыСЂЖЈЬјдЖОіШќЕФга8![]() ЕФжЕЪЧ__________ЃЎ
ЕФжЕЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзввСНШЫдкЯрЭЌЬѕМўЯТЭъГЩСЫ10ДЮЩфЛїбЕСЗЃЌСНШЫЕФГЩМЈШчЭМЫљЪОЁЃ

ИљОнвдЩЯаХЯЂЃЌећРэЗжЮіЪ§ОнШчЯТЃК
ЦНОљГЩМЈ/ЛЗ | жаЮЛЪ§/ЛЗ | ЗНВю/ЛЗ | |
Мз | ______ | 7 | 1.2 |
вв | 7 | ______ | ______ |
ЃЈ1ЃЉЭъГЩБэИёЃЛ
ЃЈ2ЃЉИљОнбЕСЗГЩМЈЃЌФуШЯЮЊбЁХЩФФвЛУћЖгдБВЮШќИќКУЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФПкДќРязАгаЗжБ№БъгаЪ§зж-3ЁЂ-1ЁЂ0ЁЂ2ЕФЫФИіаЁЧђЃЌГ§Ъ§зжВЛЭЌЭтЃЌаЁЧђУЛгаШЮКЮЧјБ№ЃЌУПДЮЪдбщЯШНСАшОљдШЃЎ
ЃЈ1ЃЉДгжаШЮШЁвЛЧђЃЌНЋЧђЩЯЕФЪ§зжМЧЮЊaЃЌдђЙигкxЕФдЊЖўДЮЗНГЬx2-2x-a+1=0гаЪЕЪ§ИљЕФИХТЪ______ЃЛ
ЃЈ2ЃЉДгжаШЮШЁвЛЧђЃЌНЋЧђЩЯЕФЪ§зжзїЮЊЕуЕФКсзјБъЃЌМЧЮЊxЃЈВЛЗХЛиЃЉЃЛдйШЮШЁвЛЧђЃЌНЋЧђЩЯЕФЪ§зжзїЮЊЕуЕФзнзјБъЃЌМЧЮЊyЃЌЪдгУЛЪїзДЭМЃЈЛђСаБэЗЈЃЉБэЪОГіЕуЃЈxЃЌyЃЉЫљгаПЩФмГіЯжЕФНсЙћЃЌВЂЧѓЕуЃЈxЃЌyЃЉТфдкЕкШ§ЯѓЯоФкЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯABCЃН30ЁуЃЌЁїCDEЪЧЕШБпШ§НЧаЮЃЌЕуDдкБпABЩЯЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуEдкБпBCЩЯЪБЃЌЧѓжЄDEЃНEBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкЁїABCФкВПЪБЃЌВТЯыEDКЭEBЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕуEдкЁїABCЭтВПЪБЃЌEHЁЭABгкЕуHЃЌЙ§ЕуEзїGEЁЮABЃЌНЛЯпЖЮACЕФбгГЄЯпгкЕуGЃЌAGЃН5CGЃЌBHЃН3ЃЎЧѓCGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЪЕЯжЧјгђНЬг§ОљКтЗЂеЙЃЌЮвЪаМЦЛЎЖдФГЯиAЁЂBСНРрБЁШѕбЇаЃШЋВПНјааИФдьЃЎИљОндЄЫуЃЌЙВашзЪН№1555ЭђдЊИФдьвЛЫљAРрбЇаЃКЭСНЫљBРрбЇаЃЙВашзЪН№230ЭђдЊЃЛИФдьСНЫљAРрбЇаЃКЭвЛЫљBРрбЇаЃЙВашзЪН№205ЭђдЊ
ЃЈ1ЃЉИФдьвЛЫљAРрбЇаЃКЭвЛЫљBРрбЇаЃЫљашЕФзЪН№ЗжБ№ЪЧЖрЩйЭђдЊЃП
ЃЈ2ЃЉИљОнЮвЪаНЬг§ОжЙцЛЎМЦЛЎНёФъЖдИУЯиAЁЂBСНРрбЇаЃНјааИФдьЃЌвЊЧѓИФдьЕФAРрбЇаЃЪЧBРрбЇаЃЕФ2БЖЖр2ЫљЃЌдкМЦЛЎЭЖШызЪН№ВЛГЌЙ§1555ЭђдЊЕФЬѕМўЯТЃЌжСЖрФмИФдьЖрЩйЫљAРрбЇаЃЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЌЗжБ№вд
ЩЯЕФвЛИіЖЏЕуЃЌЗжБ№вд![]() ЃЌ
ЃЌ![]() ЮЊБпдк
ЮЊБпдк![]() ЕФЭЌВрзїСтаЮ
ЕФЭЌВрзїСтаЮ![]() КЭСтаЮ
КЭСтаЮ![]() ЃЎЕу
ЃЎЕу![]() ЃЌ
ЃЌ![]() ЃЌ
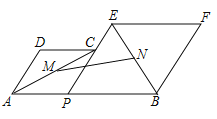
ЃЌ![]() дквЛЬѕжБЯпЩЯЃЌ
дквЛЬѕжБЯпЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЖдНЧЯп
ЗжБ№ЪЧЖдНЧЯп![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЎЕБЕу
ЕФжаЕуЃЎЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвЦЖЏЪБЃЌЕу
ЩЯвЦЖЏЪБЃЌЕу![]() ЁЂ
ЁЂ![]() жЎМфЕФОрРызюЖЬЮЊ_______ЃЎ
жЎМфЕФОрРызюЖЬЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃВЭЬќжаЃЌвЛеХзРзгПЩзј6ШЫЃЌЯжгавдЯТСНжжАкЗХЗНЪН:
ЃЈ1ЃЉЕБга5еХзРзгЪБЃЌЕквЛжжЗНЪНФмзј ШЫЃЌЕкЖўжжЗНЪНФмзј ШЫЃЎ
ЃЈ2ЃЉЕБгаnеХзРзгЪБЃЌЕквЛжжЗНЪНФмзј ШЫЃЌЕкЖўжжЗНЪНФмзј ШЫЃЎ
ЃЈ3ЃЉаТбЇЦкга200ШЫдкбЇаЃОЭВЭЃЌЕЋВЭЬќжЛга60еХетбљЕФВЭзРЃЌШєФуЪЧРЯЪІЃЌФуДђЫубЁдёвдЯТФФжжЗНЪНРДАкЗХВЭзР?ЮЊЪВУД?

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() Еу
Еу![]() гыЕу
гыЕу![]() дк
дк![]() ЕФЭЌВрЃЌЧв
ЕФЭЌВрЃЌЧв![]() ЃЎ
ЃЎ

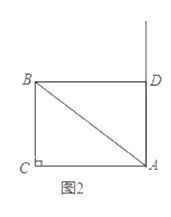
ЃЈ1ЃЉШчЭМ1ЃЌЕу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯЃЌСЌНс
жиКЯЃЌСЌНс![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎЩш
ЃЎЩш![]() Чѓ
Чѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЌаДГіздБфСП
ЕФКЏЪ§НтЮіЪНЃЌаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() гы
гы![]() ЯрЫЦЃЌШєДцдкЃЌЧѓ
ЯрЫЦЃЌШєДцдкЃЌЧѓ![]() ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() ДЙзуЮЊ
ДЙзуЮЊ![]() ЃЎНЋвдЕу
ЃЎНЋвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖЕФдВМЧЮЊ
ЮЊАыОЖЕФдВМЧЮЊ![]() ЃЎШєЕу
ЃЎШєЕу![]() ЕН
ЕН![]() ЩЯЕуЕФОрРыЕФзюаЁжЕЮЊ
ЩЯЕуЕФОрРыЕФзюаЁжЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФАыОЖЃЎ
ЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com