
【题目】如图,正方形![]() 的边长为2,点
的边长为2,点![]() 为坐标原点,边
为坐标原点,边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,点
轴上,点![]() 是
是![]() 的中点.点
的中点.点![]() 是线段
是线段![]() 上的一个点,如果将
上的一个点,如果将![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 所在直线上.
所在直线上.
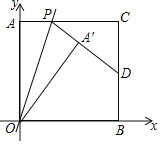
(1)若点![]() 是端点,即当点
是端点,即当点![]() 在
在![]() 点时,
点时,![]() 点的位置关系是________,
点的位置关系是________,![]() 所在的直线是__________;当点
所在的直线是__________;当点![]() 在
在![]() 点时,
点时,![]() 点的位置关系是________,
点的位置关系是________,![]() 所在的直线表达式是_________;
所在的直线表达式是_________;
(2)若点![]() 不是端点,用你所学的数学知识求出
不是端点,用你所学的数学知识求出![]() 所在直线的表达式;
所在直线的表达式;
(3)在(2)的情况下,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长为最小值?若存在,请求出点
的周长为最小值?若存在,请求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)A,y轴;B,y=x;(2)y=3x;(3)存在.由于,理由见解析.
【解析】
(1)由轴对称的性质可得出结论;
(2)连接OD,求出OD=![]() ,设点P(
,设点P(![]() ,2),PA′=
,2),PA′=![]() ,PC=
,PC=![]() ,CD=1.可得出(
,CD=1.可得出(![]() )2=(2
)2=(2![]() )2+12,解方程可得解x=
)2+12,解方程可得解x=![]() .求出P点的坐标即可得出答案;
.求出P点的坐标即可得出答案;
(3)可得出点D关于![]() 轴的对称点是D′(2,-1),求出直线PD′的函数表达式为
轴的对称点是D′(2,-1),求出直线PD′的函数表达式为![]() ,则答案可求出.
,则答案可求出.
(1)由轴对称的性质可得,若点P是端点,即当点P在A点时,A′点的位置关系是点A,
OP所在的直线是y轴;
当点P在C点时,
∵∠AOC=∠BOC=45°,
∴A′点的位置关系是点B,
OP所在的直线表达式是y=x.
故答案为:A,y轴;B,y=x;
(2)连接OD,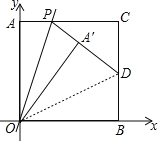
∵正方形AOBC的边长为2,点D是BC的中点,
∴OD=![]() .
.
由折叠的性质可知,OA′=OA=2,∠OA′D=90°.
∵OA′=OA= OB=2,OD公共,
∴![]() (
(![]() ),
),
∴A′D=BD=1.
设点P(![]() ,2),则PA′=
,2),则PA′=![]() ,PC=
,PC=![]() ,CD=1,
,CD=1,
∴![]() ,即(
,即(![]() )2=(
)2=(![]() )2+12,
)2+12,
解得:![]() .
.
所以P(![]() ,2),
,2),
设OP所在直线的表达式为![]() ,
,
将P(![]() ,2)代入得:
,2)代入得:![]() ,
,
解得:![]() ,
,
∴OP所在直线的表达式是![]() ;
;
(3)存在.
若△DPQ的周长为最小,
即是要PQ+DQ为最小,
作点D关于x轴的对称点是D′,
连接D′P交x轴于点Q,此时使![]() 的周长取得最小值,
的周长取得最小值,
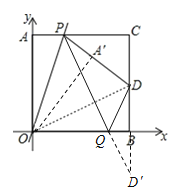
∵点D关于x轴的对称点是D′(2,![]() ),
),
∴设直线PD'的解析式为![]() ,
,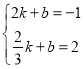 ,
,
解得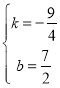 ,
,
∴直线PD′的函数表达式为![]() .
.
当![]() 时,
时,![]() .
.
∴点Q的坐标为:(![]() ,0).
,0).


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】新华中学暑假要进行全面维修,有甲、乙两个工程队共同完成,甲队单独完成这项工程所需天数是乙队单独完成所需天数的![]() ,若由甲队先做10天,剩下的工程再由甲、乙两队合作,再做30天可以完成.
,若由甲队先做10天,剩下的工程再由甲、乙两队合作,再做30天可以完成.
(1)求甲、乙两队单独完成这项工程各需多少秀?
(2)已知甲队每天的施工费用为0.84万元,乙队每天的施工费用为0.56万元,若由甲、乙两队合作,则工程预算的施工费用50万元是否够用?若不够用,需追加多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着重庆市成为旅游网红城市,重庆特产也成为游客十分喜爱的产品.洪崖洞一特产商店准备购进品牌麻花和驰名火锅底料共![]() 袋,其中购进
袋,其中购进![]() 袋品牌麻花和
袋品牌麻花和![]() 袋火锅底料共需
袋火锅底料共需![]() 元,购进
元,购进![]() 袋品牌麻花和
袋品牌麻花和![]() 袋火锅底料共需
袋火锅底料共需![]() 元.
元.
(1)商店准备将品牌麻花加价![]() ,火锅底料加价
,火锅底料加价![]() 后出售.当所有物品销售完后,若利润不低于
后出售.当所有物品销售完后,若利润不低于![]() 元,则商店至少应购进品牌麻花多少袋?
元,则商店至少应购进品牌麻花多少袋?
(2)根据销售需要临时调整销售方案,决定将品牌麻花的售价在进价基础上上涨![]() ,火锅底料的售价在进价基础上上涨
,火锅底料的售价在进价基础上上涨![]() ,在(1)中品牌麻花购买量取得最小值的情况下,将火锅底料的购买量提高
,在(1)中品牌麻花购买量取得最小值的情况下,将火锅底料的购买量提高![]() ,而品牌麻花的购买量保持不变.则全部售出后,最终可获利
,而品牌麻花的购买量保持不变.则全部售出后,最终可获利![]() 元.请求出
元.请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
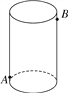
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
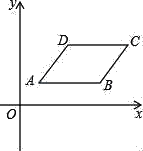
【题目】如图,在平面直角坐标系中,ABCD的边AB=2,顶点A坐标为(1,b),点D坐标为(2,b+1)
(1)点B的坐标是 ,点C的坐标是 (用b表示);
(2)若双曲线y=![]() 过ABCD的顶点B和D,求该双曲线的表达式;
过ABCD的顶点B和D,求该双曲线的表达式;
(3)若ABCD与双曲线y=![]() (x>0)总有公共点,求b的取值范围.
(x>0)总有公共点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
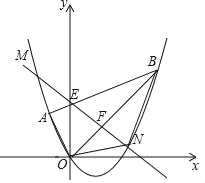
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(﹣1,0)
(1)求抛物线的解析式并作出图象;
(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com