
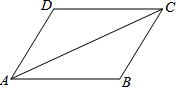
 如图,∠D=120°,AB∥DC,且AC平分∠DAB,则∠BAC=
如图,∠D=120°,AB∥DC,且AC平分∠DAB,则∠BAC=科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
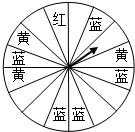 某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.
某商场设定了一个可以自由转动的转盘(转盘被等分成16个扇形),并规定:顾客在商场消费每满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄和蓝色区域,顾客就可以分别获得50元、30元和10元的购物券.如果顾客不愿意转转盘,则可以直接获得购物券15元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com