Question

9．如图，双曲线y=$\frac{k}{x}$（x＞0）经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（3，4），则△OAB的面积为18．

Answer 1

分析 将A坐标代入反比例解析式求出k的值即可；过点C作CN⊥y轴，垂足为N，延长BA，交y轴于点M，得到CN与BM平行，进而确定出三角形OCN与三角形OBM相似，根据C为OB的中点，得到相似比为1：2，确定出三角形OCN与三角形OBM面积比为1：4，利用反比例函数k的意义确定出三角形OCN与三角形AOM面积，根据相似三角形面积之比为1：4，求出三角形AOB面积即可．

解答 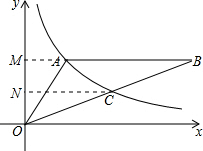解：∵点A（3，4）在双曲线y=$\frac{k}{x}$（x＞0）上，
∴k=3×4=12．
过点C作CN⊥y轴，垂足为N，延长BA，交y轴于点M，
∵AB∥x轴，
∴BM⊥y轴，
∴MB∥CN，
∴△OCN∽△OBM，
∵C为OB的中点，即$\frac{OC}{OB}$=$\frac{1}{2}$，
∴$\frac{{S}_{△OCN}}{{S}_{△OBM}}$=（$\frac{1}{2}$）²，
∵A，C都在双曲线y=$\frac{12}{x}$上，
∴S_△OCN=S_△AOM=6，
由$\frac{6}{6+{S}_{△AOB}}$=$\frac{1}{4}$，
得：S_△AOB=18，
则△AOB面积为18．
故答案是：18．

点评 此题属于反比例函数综合题，涉及的知识有：待定系数法确定函数解析式，坐标与图形性质，相似三角形的判定与性质，以及反比例函数k的意义，熟练掌握待定系数法是解本题的关键．